Ф li – Самоиндукция

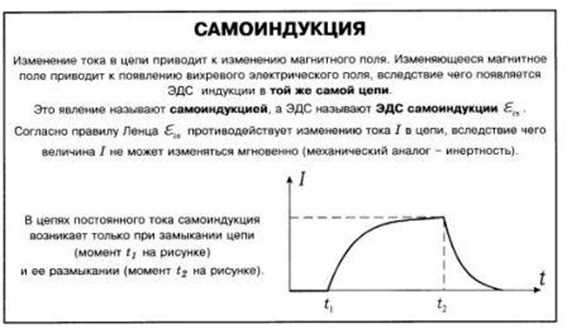
Самоиндукция

Как было установлено опытным путём, вокруг любого проводника с током создаётся магнитное поле. Мы знаем, магнитный поток Ф, проходящий через контур прямо пропорционален индукции В магнитного поля и площади S, охватываемой проводником Индукция В магнитного поля, созданного проводником с током,  в каждой точке пространства вокруг этого проводника пропорциональна силе тока I в проводнике.  Следовательно, магнитный поток Ф через данный проводящий контур (S = const) прямо пропорционален силе тока в контуре:

Ф =LI

Коэффициент пропорциональности L между силой тока I и магнитным потоком через контур называется индуктивностью контура или коэффициентом самоиндукции. Он зависит от площади, охватываемой контуром, от его формы, свойств среды, в которой находится контур.

В СИ единицей индуктивности является Генри (Гн).

L = Ф / I,

1 Гн = 1Вб / 1А.

Контур, в котором электрический ток с силой 1 Ампер создаёт магнитный поток 1 Вебер, обладает индуктивностью 1 Генри.

Постоянный ток I, протекающий через контур индуктивностью L, создаёт вокруг контура магнитный поток Ф, равный

Ф = LI

Что произойдёт с данным контуром при выключении тока?

Ток прекратится, магнитное поле исчезнет. Вспомним, исчезновение магнитного потока — это его изменение от начального значения Ф = LI до нуля. Согласно закону электромагнитной индукции, изменения магнитного потока через контур должно вызывать появление ЭДС индукции равной:

Ε_is = -∆Ф/∆t = -L (∆I/∆t)

Явление возникновения ЭДС индукции, вызванной изменением силы тока в самом контуре называется самоиндукцией.

С изменением тока в контуре пропорционально меняется и магнитный поток через поверхность, которая ограничена этим контуром. По закону электромагнитной индукции, изменение магнитного потока приводит к возбуждению в этом контуре индуктивной ЭДС.

Единицей индуктивности 1 Генри обладает такой контур, в котором при изменении силы тока на 1 Ампер за 1 секунду возникает ЭДС самоиндукции в 1 Вольт.

По правилу Ленца, ЭДС самоиндукции при уменьшении силы тока в контуре действует в направлении поддержания силы тока неизменной, при увеличении силы тока в контуре ЭДС самоиндукции препятствует увеличению тока.

Для обнаружения явления самоиндукции можно использовать электрическую цепь, представленную на схеме:

В данной цепи параллельно включены резистор и катушка с железным сердечником, последовательно с резистором и катушкой включены электрические лампы. Электрическое сопротивление резистора равно электрическому сопротивлению катушки на постоянном токе, поэтому при параллельном подключении их к источнику тока лампы должны гореть одинаково ярко.

Проведём несколько опытов. При замыкании цепи лампа в цепи катушки загорается заметно позднее, чем лампа в цепи резистора. Это можно объяснить тем, что катушка с железным сердечником обладает большой индуктивностью, ЭДС самоиндукции препятствует возрастанию тока при включении.

Обе лампы вспыхивают при отключении источника тока. Ток в цепи катушки и резистора создаёт ЭДС самоиндукции, возникающую при уменьшении силы тока в катушке. Это показывает, что магнитное поле не только способно действовать на движущие заряды, но и обладает определённым запасом энергии. Именно за счёт энергии магнитного поля возникает ток в цепи при отключении её от источника тока.

При изменении силы тока в проводнике в последнем возникает вихревое электрическое поле. Это поле тормозит электроны при возрастании силы тока и ускоряет их при убывании электрического тока в этом проводнике.

Явление самоиндукции играет очень важную роль в элекротехнике и радиотехнике. Индуктивность цепи оказывает существенное влияние на прохождение по цепи переменного электрического тока.

Остались вопросы? Не знаете, что такое самоиндукция?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Индуктивность

2014-05-23

Электрический ток I, протекающий через любой замкнутый контур, создает магнитный поток Ф, пронизывающий поверхность, ограниченную этим проводником. Если проводник неподвижен и магнитные свойства среды не меняются, магнитный поток пропорционален силе тока Ф ~ I или Ф = LI, где L — величина, характеризующая контур (например, катушку) и окружающая его среда (сердечник).

Коэффициент пропорциональности L называют индуктивностью данного контура.

? Индуктивность — это качество ведущего контура, определяемая отношением изменения потока магнитной индукции, пронизывающего контур, к изменению силы тока в нем.

? 1 генри — это индуктивность такого проводника, в котором ток силой в 1 А создает магнитный поток в 1 Вб.

Поскольку Ф = LI, из формулы получаем, что Эта формула раскрывает физический смысл индуктивности: из нее следует, что индуктивность контура численно равна ЭДС самоиндукции, возникающая в контуре при изменении силы тока на 1 А за 1 с. Поэтому индуктивность называют также коэффициентом самоиндукции.

Из последней формулы следует, что индуктивность контура равна 1 Гн, если при изменении силы тока в контуре на 1 А за 1 с в нем возникает ЭДС самоиндукции, равная 1 В.

Индуктивность

Ток I, протекающий через любой замкнутый контур, создает магнитный поток Ф, пронизывающий поверхность, ограниченную этим проводником. Если проводник неподвижен и магнитные свойства

среды не меняются, магнитный поток пропорционален силе тока: Ф ~ I или Ф = LI, где L — величина, характеризующая контур (например, катушку) и окружающая его среда (сердечник).

При таком способе введения индуктивности ее физический смысл определяют из выражения.

? Индуктивность — это собственная качество ведущего контура, определяемая отношением изменения потока магнитной индукции, пронизывающего контур, к изменению силы тока в нем.

Из последнего выражения следует, что индуктивность численно равна потоку магнитной индукции, создаваемой силой тока в 1 А. В системе СИ единицей индуктивности является генри (Гн). Эта единица названа в честь американского физика Джозефа Генри, наблюдал впервые явление самоиндукции 1832, на следующий год после открытия явления электромагнитной индукции.

категория: Физика

moykonspekt.ru

ИНДУКТИВНОСТЬ — это… Что такое ИНДУКТИВНОСТЬ?

в электродинамике (коэффициент самоиндукции) (от лат. inductio — наведение, побуждение) — параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин «И.» употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним — катушка самоиндукции).И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновениювихревого электрич. поля E(r, t )с отличной от нуля циркуляцией

по замкнутым контурам

l_i;пронизываемым магн. потоком Ф _i. Внутри проводника вихревое поле Е взаимодействует с порождающим его током и оказывает противодействие изменению магн. потока (Ленца правило). Циркуляция E_i и магн. поток Ф _i существенно зависят от выбора контура l_i внутри проводника конечной толщины. Однако при медленных движениях и квазистацнонарных процессах, когда полный ток

(j — плотностьтока) одинаков для всех нормальных сечений провода S _пр, допустим переход к усреднённым характеристикам: эдс самоиндукции E _си=<E_i> )и сцепленному с проводящим контуром магн. потоку Ф=<Ф _i>_. В предположении о том, что линии тока замыкаются сами на себя при одном обходе по контуру,

где r_^ , — радиус-векторы точек нормального сечения провода, Ф _j(r_^) — магн. поток через поверхность, ограниченную линией тока, проходящей через точку r_^, E_j(r_^) — циркуляция вектора E вдоль этой линии тока, j_n — нормальная к S_np составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должнаудовлетворять энергетич. соотношению: =E _сиI ( Р— суммарная мощность взаимодействия поля с током).Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:

Ф=L.I (в СИ), Ф=¹/_c(LI)(в системе СГС). (1)

Коэф. L и Lназ. И. Величина L измеряется в генри, L — в см.

E _си=-d/dt(LI) (в СИ), E_cи⁼-(1/с ²)(d/dt)(LI)(2) (в системе СГС).

Производная по времени от И. определяет ту часть E _си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.

W^m=¹/₂LI² (в СИ), W^m=¹/₂c²LI² (в системе СГС). (3)

Соотношение (3) позволяет различать И. внутреннюю L_i, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю L_e, связанную с внеш. магн. полем (L=L_i+L_e, L=L_i+L_e). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусамиих изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения L_i=(m₀/8p)m_il (l — длина провода, m_i — магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l₁) совпадает с осевой линией проводника, а другая (l₂) совмещена с его поверхностью:

где r₁, r₂ — радиус-векторы точек на контурах l_l,<sub>l2,m е — магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L «(m0/4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:

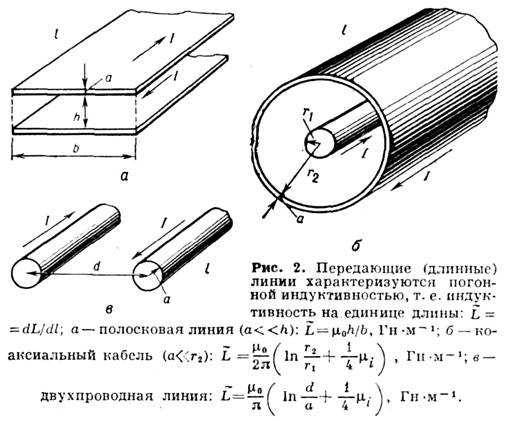
где l и а — длина и радиус провода. Это выражение обладает логарифмич. точностью — его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.

Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m0R(ln(8R/r)-2+¹/4mi), Гн, r<<R.</sub>

Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой — соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеальногосоленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j _пов=Ik (I — ток в соленоиде, k — число витков на единице длины).

Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл.-магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока I_w и эдс самоиндукции E_w связаны соотношением:

И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление R_L(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса — Кронига соотношением:

где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением R_L(w) можно пренебречь, тогда E_w и I_w сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду:

где W^m_w— усреднённая по периоду колебаний энергия ближних (квазистационарных) магн. полей (полная магн. энергия поля не определена из-за линейно растущей во времени энергии поля излучения).Если в цепи действует гармонич. сторонняя эдс , то во втором законе Кирхгофа величина E_w может быть перенесена (со сменой знака) в правую часть равенства:

где С —ёмкость, включённая в цепь. Соотношение (9) позволяет трактовать величину Z_L=iwLкак индуктивную часть импеданса цепи (при атом Z_C=-i/w С —ёмкостная, a Z_R=R— активная части полного импеданса Z=Z_L+Z_C+Z_R). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении , а при параллельном При описании сильноточных цепей часто требуется обобщение понятия И. на случай нелинейных систем. Если неподвижный проводящий контур помещён всреду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна:

Величина L _Д(I)=d Ф /dIназ. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид:

B линейном приближении (при I «0) L _Д «L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е., Основы теории электричества9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

dic.academic.ru

Формулы по физике для ЕГЭ и 7-11 класса

Рубрика: Подготовка к ЕГЭ по физике

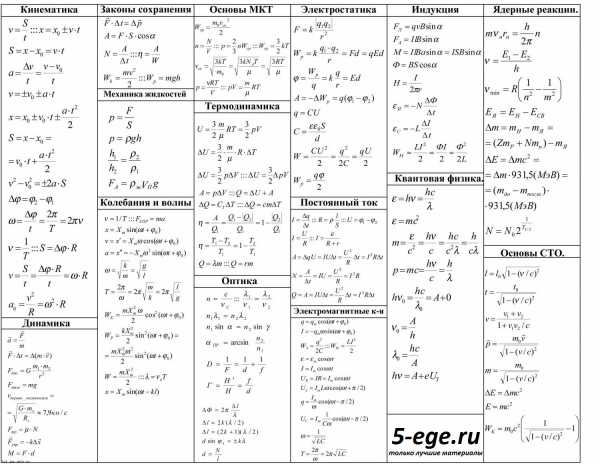
Шпаргалка с формулами по физике для ЕГЭ

и не только (может понадобиться 7, 8, 9, 10 и 11 классам).

Для начала картинка, которую можно распечатать в компактном виде.

Механика

1. Давление                      Р=F/S
2. Плотность                   ρ=m/V
3. Давление на глубине жидкости   P=ρ∙g∙h
4. Сила тяжести                       Fт=mg
5. 5. Архимедова сила                 Fa=ρ_ж∙g∙Vт
6. Уравнение движения  при равноускоренном  движении

X=X₀+υ₀∙t+(a∙t²)/2                    S= (υ²—υ₀²)^{/2а         S= (υ+υ₀) ∙t /2}

1. Уравнение скорости  при равноускоренном движении υ=υ₀+a∙t
2. Ускорение            a=(υ—υ ₀)/t
3. Скорость при движении по окружности υ =2πR/Т
4. Центростремительное ускорение  a=υ²/R
5. Связь периода с частотой ν=1/T=ω/2π
6. II закон Ньютона                F=ma
7. Закон Гука                          Fy=-kx
8. Закон Всемирного тяготения  F=G∙M∙m/R²
9. Вес тела, движущегося с ускорением а↑      Р=m(g+a)
10. Вес тела, движущегося с ускорением а↓      Р=m(g-a)
11. Сила трения                     Fтр=µN
12. Импульс тела                       p=mυ
13. Импульс силы                     Ft=∆p
14. Момент силы                    M=F∙ℓ
15. Потенциальная энергия тела, поднятого над землей Eп=mgh
16. Потенциальная энергия упруго деформированного тела Eп=kx²/2
17. Кинетическая энергия тела Ek=mυ²/2
18. Работа            A=F∙S∙cosα
19. Мощность     N=A/t=F∙υ
20. Коэффициент полезного действия η=Aп/Аз
21. Период колебаний математического маятника T=2π√ℓ/g
22. Период колебаний пружинного маятника T=2 π √m/k
23. Уравнение гармонических колебаний  Х=Хmax∙cos ωt
24. Связь длины волны, ее скорости и периода λ= υТ

Молекулярная физика и термодинамика

1. Количество вещества              ν=N/ Na
2. Молярная масса                           М=m/ν
3. Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
4. Основное уравнение МКТ      P=nkT=1/3nm₀υ²
5. Закон Гей – Люссака (изобарный процесс)    V/T =const
6. Закон Шарля (изохорный процесс)    P/T =const
7. Относительная влажность φ=P/P₀∙100%
8. Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
9. Работа газа A=P∙ΔV
10. Закон Бойля – Мариотта (изотермический процесс)    PV=const
11. Количество теплоты при нагревании  Q=Cm(T₂-T₁)
12. Количество теплоты при плавлении   Q=λm
13. Количество теплоты при парообразовании  Q=Lm
14. Количество теплоты при сгорании топлива  Q=qm
15. Уравнение состояния идеального газа PV=m/M∙RT
16. Первый закон термодинамики   ΔU=A+Q
17. КПД тепловых двигателей         η= (Q₁ — Q₂)/ Q₁
18. КПД идеал. двигателей  (цикл Карно)     η= (Т₁ — Т₂)/ Т₁

https://5-ege.ru/formuly-po-fizike-dlya-ege/

Электростатика и электродинамика – формулы по физике

1. Закон Кулона F=k∙q₁∙q₂/R²
2. Напряженность электрического поля E=F/q
3. Напряженность эл. поля точечного заряда E=k∙q/R²
4. Поверхностная плотность зарядов             σ = q/S
5. Напряженность эл. поля бесконечной плоскости E=2πkσ
6. Диэлектрическая проницаемость ε=E₀/E
7. Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R
8. Потенциал φ=W/q
9. Потенциал точечного заряда φ=k∙q/R
10. Напряжение U=A/q
11. Для однородного электрического поля U=E∙d
12. Электроемкость C=q/U
13. Электроемкость плоского конденсатора C=S∙ε∙ε₀/d
14. Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
15. Сила тока I=q/t
16. Сопротивление проводника R=ρ∙ℓ/S
17. Закон Ома для участка цепи I=U/R
18. Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R
19. Законы паралл. соед.   U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R
20. Мощность электрического тока P=I∙U
21. Закон Джоуля-Ленца Q=I²Rt
22. Закон Ома для полной цепи I=ε/(R+r)
23. Ток короткого замыкания (R=0)      I=ε/r
24. Вектор магнитной индукции B=Fmax/ℓ∙I
25. Сила Ампера Fa=IBℓsin α
26. Сила Лоренца Fл=Bqυsin α
27. Магнитный поток Ф=BSсos α      Ф=LI
28. Закон электромагнитной индукции Ei=ΔФ/Δt
29. ЭДС индукции в движ проводнике Ei=Вℓυsinα
30. ЭДС самоиндукции Esi=-L∙ΔI/Δt
31. Энергия магнитного поля катушки Wм=LI²/2
32. Период колебаний кол. контура T=2π ∙√LC
33. Индуктивное сопротивление X_L=ωL=2πLν
34. Емкостное сопротивление Xc=1/ωC
35. Действующее значение силы тока Iд=Imax/√2,
36. Действующее значение напряжения Uд=Umax/√2
37. Полное сопротивление Z=√(Xc-X_L)²+R²

Оптика

1. Закон преломления света     n₂₁=n₂/n₁= υ ₁/ υ ₂
2. Показатель преломления      n₂₁=sin α/sin γ
3. Формула тонкой линзы       1/F=1/d + 1/f
4. Оптическая сила линзы       D=1/F
5. max интерференции: Δd=kλ,
6. min интерференции: Δd=(2k+1)λ/2
7. Диф.решетка             d∙sin φ=k λ

Квантовая физика

1. Ф-ла Эйнштейна для фотоэффекта  hν=Aвых+Ek, Ek=U_зе
2. Красная граница фотоэффекта ν_к = Aвых/h
3. Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

1. Закон радиоактивного распада N=N₀∙2^—t/T
2. Энергия связи атомных ядер

E_CB=(Zm_p+Nm_n-Mя)∙c²

СТО

1. t=t₁/√1-υ²/c²
2. ℓ=ℓ₀∙√1-υ²/c²
3. υ₂=(υ₁+υ)/1+ υ₁∙υ/c²
4. Е = mс²

Скачать эти формулы в doc: formuly-po-fizike-5-ege.ru (файл расположен на 5-ege.ru).

Рекомендуем:

5-ege.ru

Индуктивность — Физическая энциклопедия

ИНДУКТИВНОСТЬ в электродинамике (коэффициент самоиндукции) (от лат. inductio — наведение, побуждение) — параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин «И.» употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним — катушка самоиндукции). И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновению вихревого электрич. поля E(r, t)с отличной от нуля циркуляцией

по замкнутым контурам l_i; пронизываемым магн. потоком Ф_i. Внутри проводника вихревое поле Е взаимодействует с порождающим его током и оказывает противодействие изменению магн. потока (Ленца правило ).Циркуляция E_i и магн. поток Ф_i существенно зависят от выбора контура l_i внутри проводника конечной толщины. Однако при медленных движениях и квазистацнонарных процессах, когда полный ток

(j — плотность тока) одинаков для всех нормальных сечений провода S_пр, допустим переход к усреднённым характеристикам: эдс самоиндукции E_си=<E_i>)и сцепленному с проводящим контуром магн. потоку Ф=<Ф_i>_. В предположении о том, что линии тока замыкаются сами на себя при одном обходе по контуру,

где r_^ , — радиус-векторы точек нормального сечения провода, Ф_j(r_^) — магн. поток через поверхность, ограниченную линией тока, проходящей через точку r_^, E_j(r_^) — циркуляция вектора E вдоль этой линии тока, j_n — нормальная к S_np составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должна удовлетворять энергетич. соотношению: =E_сиI (Р — суммарная мощность взаимодействия поля с током). Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:

Ф=L.I (в СИ), Ф=¹/_c(LI) (в системе СГС). (1)

Коэф. L и L наз. И. Величина L измеряется в генри, L — в см. Для эдс самоиндукции справедливо соотношение

E_си=-d/dt(LI) (в СИ), E_cи⁼-(1/с²)(d/dt)(LI) (2) (в системе СГС).

Производная по времени от И. определяет ту часть E_си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. В известном смысле И. характеризует инерционность цепи по отношению к изменению в ней тока и является электродинамич. аналогом массы тела в механике (при этом I сопоставляется со скоростью тела). В частности, для цепей пост. тока энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.

W^m=¹/₂LI² (в СИ), W^m=¹/₂c²LI² (в системе СГС). (3)

Соотношение (3) позволяет различать И. внутреннюю L_i, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю L_e, связанную с внеш. магн. полем (L=L_i+L_e, L=L_i+L_e). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусами их изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения L_i=(m₀/8p)m_il (l — длина провода, m_i — магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l₁) совпадает с осевой линией проводника, а другая (l₂) совмещена с его поверхностью:

где r₁, r₂ — радиус-векторы точек на контурах l_l,<sub>l2, mе — магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L»(m0/4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:

где l и а — длина и радиус провода. Это выражение обладает логарифмич. точностью — его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.

Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m0R(ln(8R/r)-2+¹/4mi), Гн, r<<R.</sub>

Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой — соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеального соленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j_пов=Ik (I — ток в соленоиде, k — число витков на единице длины).

Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл—магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока I_wи эдс самоиндукции E_w связаны соотношением:

И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление R_L(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса — Кронига соотношением:

где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением R_L(w) можно пренебречь, тогда E_w и I_w сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду:

где W^m_w — усреднённая по периоду колебаний энергия ближних (квазистационарных) магн. полей (полная магн. энергия поля не определена из-за линейно растущей во времени энергии поля излучения). Если в цепи действует гармонич. сторонняя эдс , то во втором законе Кирхгофа величина E_w может быть перенесена (со сменой знака) в правую часть равенства:

где С — ёмкость, включённая в цепь. Соотношение (9) позволяет трактовать величину Z_L=iwL как индуктивную часть импеданса цепи (при атом Z_C=-i/wС — ёмкостная, a Z_R=R — активная части полного импеданса Z=Z_L+Z_C+Z_R). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении , а при параллельном При описании сильноточных цепей часто требуется обобщение понятия И. на случай нелинейных систем. Если неподвижный проводящий контур помещён в среду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна:

Величина L_Д(I)=dФ/dI наз. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид:

B линейном приближении (при I»0) L_Д»L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е., Основы теории электричества 9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин

      Предметный указатель      >>   

www.femto.com.ua

Формулы по физике

Уравнение скорости при равноускоренном движении υ=υ₀+a∙t

Ускорение a=(υ—υ ₀)/t

Скорость при движении по окружности υ=2πR/Т

Центростремительное ускорение a=υ²/R

Связь периода с частотой ν=1/T=ω/2π

II закон Ньютона F=ma

Закон Гука Fy=-kx

Закон Всемирного тяготения F=G∙M∙m/R²

Вес тела, движущегося с ускорением а↑ Р=m(g+a)

Вес тела, движущегося с ускорением а↓ Р=m(g-a)

Сила трения Fтр=µN

Импульс тела p=mυ

Импульс силы Ft=∆p

Момент силы M=F∙ℓ

Потенциальная энергия тела, поднятого над землей Eп=mgh

Потенциальная энергия упруго деформированного тела Eп=kx²/2

Кинетическая энергия тела Ek=mυ²/2

Работа A=F∙S∙cosα

Мощность N=A/t=F∙υ

Коэффициент полезного действия η=Aп/Аз

Период колебаний математического маятника T=2π√ℓ/g

Период колебаний пружинного маятника T=2 π √m/k

Уравнение гармонических колебаний Х=Хmax∙cos ωt

Связь длины волны, ее скорости и периода λ= υТ

Количество вещества ν=N/ Na

Молярная масса М=m/ν

Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT

Основное уравнение МКТ P=nkT=1/3nm₀υ²

Закон Гей – Люссака (изобарный процесс) V/T =const

Закон Шарля (изохорный процесс) P/T =const

Относительная влажность φ=P/P₀∙100%

Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT

Работа газа A=P∙ΔV

Закон Бойля – Мариотта (изотермический процесс) PV=const

Количество теплоты при нагревании Q=Cm(T₂-T₁)

Количество теплоты при плавлении Q=λm

Количество теплоты при парообразовании Q=Lm

Количество теплоты при сгорании топлива Q=qm

Уравнение состояния идеального газа PV=m/M∙RT

Первый закон термодинамики ΔU=A+Q

КПД тепловых двигателей η= (Q₁ — Q₂)/ Q₁

КПД идеал. двигателей (цикл Карно) η= (Т₁ — Т₂)/ Т₁

Закон Кулона F=k∙q₁∙q₂/R²

Напряженность электрического поля E=F/q

Напряженность эл. поля точечного заряда E=k∙q/R²

Поверхностная плотность зарядов σ = q/S

Напряженность эл. поля бесконечной плоскости E=2πkσ

Диэлектрическая проницаемость ε=E₀/E

Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R

Потенциал φ=W/q

Потенциал точечного заряда φ=k∙q/R

Напряжение U=A/q

Для однородного электрического поля U=E∙d

Электроемкость C=q/U

Электроемкость плоского конденсатора C=S∙ε∙ε₀/d

Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2

Сила тока I=q/t

Сопротивление проводника R=ρ∙ℓ/S

Закон Ома для участка цепи I=U/R

Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R

Законы паралл. соед. U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R

Мощность электрического тока P=I∙U

Закон Джоуля-Ленца Q=I²Rt

Закон Ома для полной цепи I=ε/(R+r)

Ток короткого замыкания (R=0) I=ε/r

Вектор магнитной индукции B=Fmax/ℓ∙I

Сила Ампера Fa=IBℓsin α

Сила Лоренца Fл=Bqυsin α

Магнитный поток Ф=BSсos α Ф=LI

Закон электромагнитной индукции Ei=ΔФ/Δt

ЭДС индукции в движ проводнике Ei=Вℓυsinα

ЭДС самоиндукции Esi=-L∙ΔI/Δt

Энергия магнитного поля катушки Wм=LI²/2

Период колебаний кол. контура T=2π ∙√LC

Индуктивное сопротивление X_L=ωL=2πLν

Емкостное сопротивление Xc=1/ωC

Действующее значение силы тока Iд=Imax/√2,

Действующее значение напряжения Uд=Umax/√2

Полное сопротивление Z=√(Xc-X_L)²+R²

studfiles.net

F*Li — Бинарные химические соединения — Каталог статей — «МАТИ»

(LiF)₂

(LiF)₃

LiF

 

Литий непосредственно соединяется с галогенами (с йодом при нагревании). Во всех случаях взаимодействия с галоидами продуктом реакции является соответствующая соль МГ.

Фторид лития LiF – бесцветные кристаллы, т. пл.   849⁰С, ∆Н_обр⁰ = — 618,3 кДж/моль. Плохо растворим в воде. Хорошо растворяется в концентрированной фтористоводородной кислоте, H₂SO₄и HNO₃.

Получают LiF взаимодействием LiOH или солей лития с HF,  NH₄F, NH₄HF₂ или их водными растворами.

LiF – материал термолюминесцентных дозиметров  рентгеновского  и γ-излучения, оптический материал, компонент электролитов (при получении алюминия и фтора), эмалей, глазурей, керамики, люминофоров и лазерных материалов, промежуточный продукт для получения фторометаллатов, например Li[BeF₄].

Фтори́д ли́тия, фто́ристый ли́тий — химическое соединение лития и фтора с формулой LiF. При нормальных условиях — белый порошок или прозрачный бесцветный кристалл, негигроскопичный, почти не растворим в воде. Растворяется в азотной и плавиковой кислоте.

Получение

• Используя плохую растворимость фторида лития его легко получить обменными реакциями:

• Так же можно получить взаимодействием гидроокиси и кислоты:

Физические свойства

Фторид лития — это белый порошок или прозрачные бесцветные кристаллы, принадлежат к кубической сингонии, пространственная группа F m3m, параметры а = 0,40279 нм, Z = 4.

Плохо растворяется в воде (0,120 г/100 мл при 0 °С^[1]), при повышении температуры растворимость несколько повышается (0,134 г/100 мл при 25 °С^[1]; 0,1357 г/100 мл при 35 °С). Произведение растворимостиKsp = 1,84·10⁻³ (при 25 °С)^[1].

Плавится при 848,2 °С^[1]; плотность расплава 1,81 г/см^3[1], коэффициент объёмного расширения жидкого LiF составляет 4,90·10⁻⁴ К⁻¹·г/см^3[1].

Теплопроводность при стандартных условиях 4,01 Вт/(м·K), при гелиевой температуре (4,2 К) 620 Вт/(м·K), при20 К 1800 Вт/(м·K), при повышении температуры до азотной (77 К) теплопроводность снижается до 150 Вт/(м·K)^[1].

Фторид лития диамагнитен, его молярная магнитная восприимчивость равна −10,1·10⁻⁶ см³/моль^[1].Относительная диэлектрическая проницаемость составляет 9,00 (при комнатной температуре, в диапазоне10²—10⁷ Гц)^[1].

Межъядерное расстояние в молекуле LiF составляет 1,5639 нм (в газовой фазе)^[1], коэффициент упругости связи2,50 Н/см^[1]. Электрическая поляризуемость молекулы равна 10,8·10⁻²⁴ см^3[1].

Химические свойства

• Растворяется в концентрированных сильных кислотах:

• Реагирует с оксидами и гидроксидами щелочноземельных металлов:

Применение

Фторид лития обладает очень высокой прозрачностью от ультрафиолетовой до инфракрасной области спектра(0,12…6 мкм)^[2], поэтому он используется в ультрафиолетовой (в том числе в области вакуумного ультрафиолета, где его прозрачность превосходит все прочие оптические материалы) и инфракрасной оптике. Кроме того, он используется для измерения доз облучения методом термолюминесцентной дозиметрии. Монокристаллы фторида лития используются для рентгеновских монохроматоров и для изготовления высокоэффективных (КПД 80 %) лазеров на центрах свободной окраски. Лазер F⁻₂:LiF даёт инфракрасное излучение с длиной волны 1120 нм.

Проявляет слабые сцинтилляционные свойства. Диэлектрик; характеризуется высоким удельным электрическим сопротивлением вследствие большой ширины запрещённой зоны.

 

Монокристалл фторида лития в стакане воды.

Высокая теплота плавления (1044 кДж/кг) позволяет использовать фторид лития как материал для хранения тепловой энергии^[3]. При плавлении увеличивает свой объём на 22 %. Жидкий фторид лития вызывает быструю коррозию металлов. Фторид лития-7 применяют для растворения соединений урана и тория непосредственно в реакторах.

Результаты поиска:

Результаты поиска:

 

mati-himia.3dn.ru