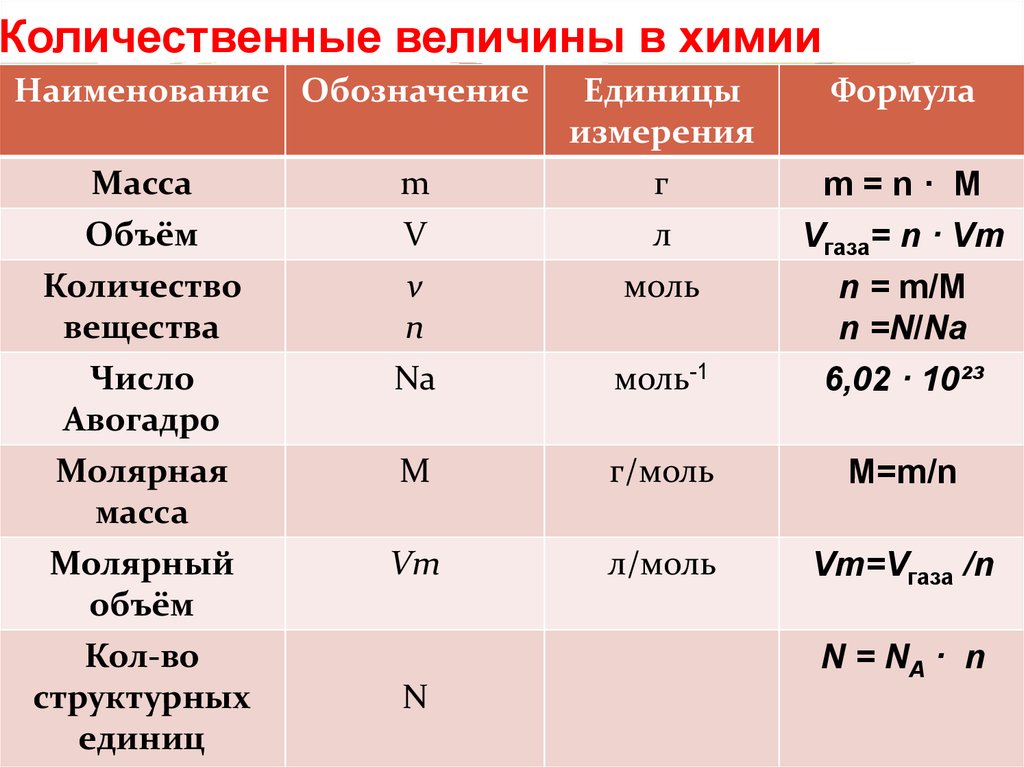
Профессиональные болезни. Зарин, зоман, V-газы
Профессиональные болезни. Зарин, зоман, V-газы
По химической структуре отравляющие вещества нервно-паралитического действия принадлежат к фосфорорганическим веществам (ФОВ). К ним относятся зарин, зоман, V-газы.
Кроме отравляющих веществ, синтезировано и продолжает синтезироваться большое количество фосфорорганических веществ мирного назначения. Это прежде всего фосфорорганические инсектициды (хлорофос, тиофос, метафос, карбофос, фосамид и др.), фосфорорганические лекарственные средства (пирофос, фосфакол, армин, фосарбин, фадаман и др.), фосфорорганические присадки к смазочным маслам, синтетическим волокнам, фосфорорганические полимеры.
Фосфорорганические отравляющие вещества — это сложные эфиры фосфорных кислот (орто- и пирофосфорной). Так, зарин — изоприловый эфир.
Зарин и зоман бесцветные (или слегка желтоватые) жидкости с характерным для каждого вещества запахом; удельный вес этих веществ несколько выше единицы (1,02—1,1).
Зарин и зоман малоустойчивы в щелочной среде: 8—10%-ные растворы едких щелочей (едкого калия и едкого натрия), а также 10%-ный раствор аммиака в воде быстро разрушают отравляющее вещество.
Химическое название V-газов — фосфорилтиохолины. В качестве представителя этой подгруппы фосфорорганических веществ можно привести О-этил-3-диметиламиноэтилметил-тиофосфат. Это вещество — бесцветная жидкость, плохо растворимая в воде, хорошо — в органических растворителях, горючих, смазочных веществах. Хорошо проникает в резиновые изделия и впитывается лакокрасочными покрытиями. Ввиду малой летучести (10—8 мг/л при температуре 20°С) долго удерживается на местности.
V-газы, зоман, зарин — стойкие отравляющие вещества.
При применении этих газов поражения будут происходить чаще всего при попадании капельно-жидкого вещества на кожные покровы или путем ингаляции паров этих ОВ.
Смертельные концентрации и дозы: ингаляционная доза зарина составляет 0,06; зомана — 0,002; V-газов — 0,001.
Все представители ФОВ обладают выраженным кумулятивным действием.
Соединения, встречаемые в природе и на производстве, применялись в качестве химического оружия.
Поступление и распространение в организме. Входными воротами для ФОВ являются кожа, органы дыхания, конъюнктива, органы пищеварения. Попадая в организм и находясь в крови, ФОВ оказываются в неблагоприятных условиях, так как в щелочной среде неустойчивы, а кровь обладает слабощелочной реакцией.
Та часть ОВ, которая не связывается с биохимическими структурами, через некоторое время обезвреживается в крови. Предполагается, что процесс разрушения ФОВ может катализироваться ферментами. Продукты превращения ФОВ в виде простейших соединений (в частности, фосфора) удаляются почками.
Продукты превращения ФОВ в виде простейших соединений (в частности, фосфора) удаляются почками.
Клиническая картина
Документ показан в сокращенном демонстрационном режиме
Чтобы продолжить, выберите ниже один из вариантов оплаты
Доступ к документам и консультации
от ведущих специалистов
Подписаться
Вы можете купить этот документ
Как купить документ?
Получить доступ
150 тг
Газоанализатор VX-газов
VX-газы
Отравляющие вещества боевого назначения делятся на несколько групп, VX-газ относится к группе нервно-паралитических соединений серии V. Он имеет очень сложное и длинное название – O-этил-S-β-диизопропиламиноэтилметилфосфонат, являясь, по сути, сложным эфиром метилфосфоновой кислоты, его упрощенная химическая формула – C11H26NO2PS. Газ был получен в процессе работы над сельскохозяйственным пестицидом амитоном в 1955 году.
Газ был получен в процессе работы над сельскохозяйственным пестицидом амитоном в 1955 году.
Физические и химические особенности
Хотя VX называют газом, в нормальных условиях соединение находится в виде малолетучей маслянистой жидкости, то есть, оно выделяет незначительное количество паров. Газосигнализатор VX-газов реагирует не столько на пары соединения, сколько на распыленный в воздухе аэрозоль.
VX относиться к высококипящим веществам, его температура кипения 298°C, температурная граница между твердым и жидким состоянием -39°C. Пары соединения более чем в 9 раз тяжелее воздуха, обладает гигроскопичностью, растворимость в воде около 5%. Вещество неплохо растворяется в жирах и смешивается с органическими растворителями, легко проникает в ткани, растения и пористые структуры, где может сохраняться долгое время, обратная диффузия может вызвать вторичное загрязнение очищенных поверхностей.
Тяжелые молекулы эфира считаются химически стабильными, при кратковременном нагревании, уровень пиролиза незначительный. При температуре 150°C, распад вещества идет с низкой скоростью – 50% за 1,5 суток, дальнейшее нагревание увеличивает скорость разложения в разы, при температуре около 300°C время процесса измеряется секундами. Период полураспада посредством гидролиза при температуре 25°C, составляет почти год – 350 суток.
При температуре 150°C, распад вещества идет с низкой скоростью – 50% за 1,5 суток, дальнейшее нагревание увеличивает скорость разложения в разы, при температуре около 300°C время процесса измеряется секундами. Период полураспада посредством гидролиза при температуре 25°C, составляет почти год – 350 суток.
Действие на организм и способы защиты
Поражение организма VX-газом проявляется в виде нарушения связи между нервной системой и мышцами. Он провоцирует холинергический криз, нарушая ход электрохимических реакций – вызывает непрерывную активацию рецепторов. Подобное воздействие имеет тяжелые последствия, очень часто заканчивающиеся смертью человека.
Вещество относится к 1-му классу опасности, его ПДК для предприятий, занимающихся уничтожением химического оружия, составляет 5,0 x 10(-6) мг/м3 – показатель очень низкий, для его определения потребуется высокочувствительный датчик VX-газов. Поражение этим веществом возможно через кожу, глаза или органы дыхания. При контакте жидкости с кожей или слизистой оболочкой глаз первые признаки могут появиться в течение минут, а могут задержаться на несколько часов, при вдыхании аэрозоли, отравление проявляется практически сразу.
Поражение этим веществом возможно через кожу, глаза или органы дыхания. При контакте жидкости с кожей или слизистой оболочкой глаз первые признаки могут появиться в течение минут, а могут задержаться на несколько часов, при вдыхании аэрозоли, отравление проявляется практически сразу.
Тяжесть отравления напрямую зависит от времени контакта с веществом. При средней степени воздействия, наблюдается миоз (сужение зрачков), затрудненное дыхание, головная боль, обильные выделения из носа и слюноотделение, потливость, рвота, мышечные судороги. В тяжелых случаях к перечисленным симптомам добавляются недержание, конвульсии и паралич.
От поражения VX-газами спасают индивидуальные средства защиты, их своевременное применение возможно только при условии надежного контроля окружающего пространства. Научно-производственная фирма ИНКРАМ предлагает эффективныq и точныq газоанализатор VX-газов Эдельвейс.
Стационарное исполнение:
Мобильное исполнение:
Газовые законы: Обзор — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1517
Созданные в начале 17 века газовые законы помогали ученым определять объемы, количество, давление и температуру при работе с газами.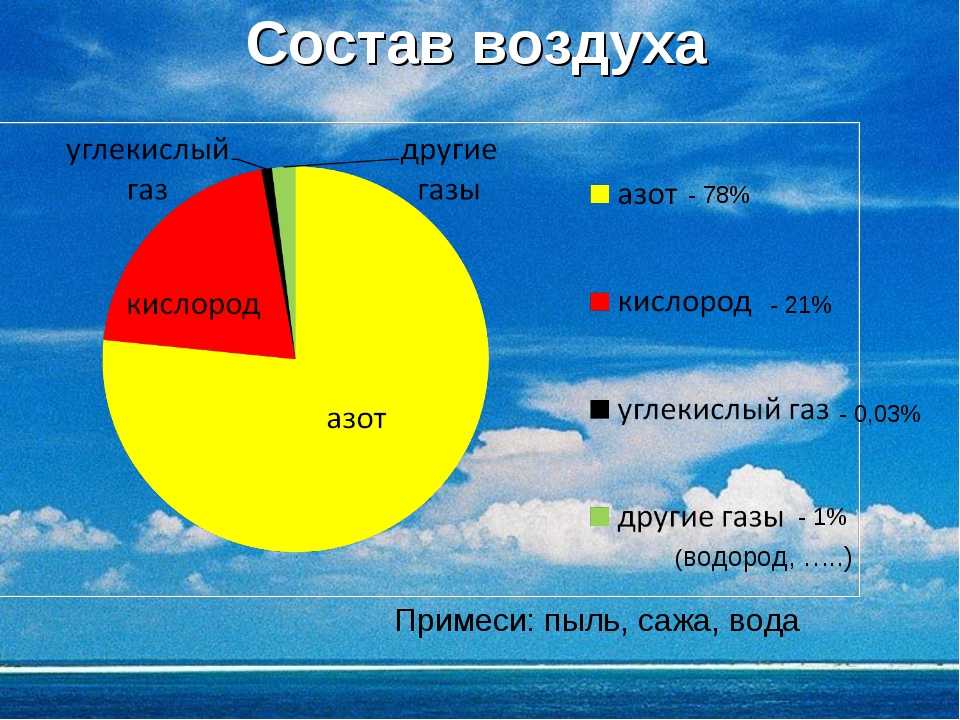 Газовые законы состоят из трех основных законов: закона Чарльза, закона Бойля и закона Авогадро (все они позже будут объединены в общее газовое уравнение и закон идеального газа).
Газовые законы состоят из трех основных законов: закона Чарльза, закона Бойля и закона Авогадро (все они позже будут объединены в общее газовое уравнение и закон идеального газа).
Введение
Три фундаментальных газовых закона раскрывают взаимосвязь между давлением, температурой, объемом и количеством газа. Закон Бойля говорит нам, что объем газа увеличивается с уменьшением давления. Закон Чарльза говорит нам, что объем газа увеличивается с повышением температуры. А закон Авогадро говорит нам, что объем газа увеличивается по мере увеличения количества газа. Закон идеального газа представляет собой комбинацию трех простых газовых законов.
Идеальные газы
Идеальный газ, или совершенный газ, является теоретической субстанцией, которая помогает установить взаимосвязь между четырьмя газовыми переменными: давлением (P),
- Частицы в газе чрезвычайно малы, поэтому газ не занимает места.

- Идеальный газ имеет постоянное, хаотическое и прямолинейное движение.
- Нет сил между частицами газа. Частицы только упруго сталкиваются друг с другом и со стенками сосуда.
Реальные газы
Реальный газ, напротив, имеет реальный объем и столкновение частиц не является упругим, поскольку между частицами существуют силы притяжения. В результате объем реального газа намного больше, чем у идеального газа, а давление реального газа ниже, чем у идеального газа. Все реальные газы ведут себя как идеальные газы при низком давлении и относительно высокой температуре.
Коэффициент сжимаемости (Z) (Z) говорит нам, насколько реальные газы отличаются от поведения идеальных газов.
\[ Z = \dfrac{PV}{nRT} \]
Для идеальных газов \( Z = 1 \). Для реальных газов \( Z\neq 1 \).
Закон Бойля
В 1662 году Роберт Бойль обнаружил корреляцию между Давлением (P) и Объемом (V) (при условии, что Температура (T) и 90 032 Количество газа(n) осталось константа):
\[ P\propto \dfrac{1}{V} \rightarrow PV=x \]
где x — константа, зависящая от количества газа при данной температуре.
- Давление обратно пропорционально объему
Другая форма уравнения (при наличии двух наборов условий и сопоставлении обеих констант друг с другом), которая может помочь в решении задач:
Образец газа объемом 17,50 мл находится под давлением 4500 атм. Какой будет объем, если давление станет 1500 атм при фиксированном количестве газа и температуре?
Раствор
\[ V_2= \dfrac {P_1 \centerdot V_1}{P_2} \] \[ =\dfrac{4,500 атм \centerdot 17,50 мл}{1,500 атм} \] \[ = 52,50 мл \]
Закон Шарля
В 1787 году французские физики Жак Шарль обнаружили корреляцию между Температура (T) и Объем (V) (при условии, что Давление (P) и Количество Газ(н) остаются постоянными):
\[ V \propto T \rightarrow V=yT \]
где y — константа, зависящая от количества газа и давления. Объем прямо пропорционален температуре
Объем прямо пропорционален температуре
Другая форма уравнения (при условии, что есть 2 набора условий и привязка обеих констант друг к другу), которая может помочь решить проблемы:
\[ \dfrac{V_1}{T_1} = y = \dfrac{V_2}{T_2} \]
| Пример 1.2 |
|---|
Образец углекислого газа в насосе имеет объем 20,5 мл и температуру 40,0 o C. Если количество газа и давление остаются постоянными, найдите новый объем углекислого газа в насосе при повышении температуры до 65,0 o C. СУТИОН \[ V_2=\dfrac{V_1 \centerdot T_2}{T_1}\] \[ =\dfrac{20,5 мл \centerdot (60+273,15K)}{40+273,15K}\] \[ = 22,1 мл \] |
Закон Авогадро. остаются постоянными):
\[ V \propto n \rightarrow V = zn\]
где z — константа, зависящая от давления и температуры.
- Объем (V) прямо пропорционален количеству газа (n)
Другая форма уравнения (при условии, что есть 2 набора условий и привязка обеих констант друг к другу), которая может помочь решить проблемы:
\[ \dfrac{P_1}{n_1} = z= \dfrac{P_2}{n_2}\]
| Пример 1.3 |
|---|
3,80 г газообразного кислорода в насосе имеет объем 150 мл. постоянная температура и давление. Если в насос добавлено 1,20 г газообразного кислорода. Каким будет новый объем газообразного кислорода в насосе, если температура и давление останутся постоянными? РастворV 1 =150 мл \[ n_1= \dfrac{m_1}{M_кислород} \] 9-1} \] \[ = 197мл\] |
Закон идеального газа представляет собой комбинацию трех законов простого газа. Установив все три закона прямо или обратно пропорционально Volume, вы получите:
\[ V \propto \dfrac{nT}{P}\]
Далее, заменив знак прямо пропорционально на константу (R), вы получите:
\[ V = \dfrac{RnT}{P}\]
И, наконец, получим уравнение:
\[ PV = nRT \]
где P= абсолютное давление идеального газа
- V= объем идеального газа
- n = количество газа
- T = абсолютная температура
- R = газовая постоянная
Здесь R называется газовой постоянной. Значение R определяется по результатам эксперимента. Его числовое значение изменяется с единицами измерения.
Значение R определяется по результатам эксперимента. Его числовое значение изменяется с единицами измерения.
R = газовая постоянная = 8,3145 Дж · моль -1 · K -1 (единица СИ)
= 0,082057 л · атм·K — 1 · моль — 1
| Пример 1.4 |
|---|
При 655 мм рт. ст. и 25,0 o C образец газообразного хлора имеет объем 750 мл. Сколько молей газообразного хлора при этих условиях?
н=? Решение\[ n=\frac{PV}{RT} \] 9-1 \centerdot (25+273,15K) }\] \[ =0,026 моль\] |
Расчет газовой постоянной, R
Числовое значение газовой постоянной, R, можно получить из уравнения идеального газа PV=nRT. При стандартной температуре и давлении, где температура 0 o С, или 273,15 К, давление при 1 атм, а при объеме 22,4140 л,
При стандартной температуре и давлении, где температура 0 o С, или 273,15 К, давление при 1 атм, а при объеме 22,4140 л,
\[ R= \frac{PV}{RT} \]
\[ \frac{1 атм \centerdot 22,4140L}{1 моль \centerdot 273,15K} \] 9{-1} \]
Общее уравнение газа
В ситуации с идеальным газом \( \frac{PV}{nRT} = 1 \) (при условии, что все газы «идеальны» или совершенны). В случаях, когда \( \frac{PV}{nRT} \neq 1 \) или при наличии нескольких наборов условий (давление (P), объем (V), количество газа (n) и температура (T)) , используйте общее газовое уравнение:
Предполагая 2 набора условий:
Начальный случай: Окончательный случай:
\[ P_iV_i = n_iRT_i \; \; \; \; \; \; P_fV_f = n_fRT_f \]
Присвоив обеим сторонам значение R (которое является константой с одинаковым значением в каждом случае), можно получить:
\[ R= \dfrac{P_iV_i}{n_iT_i} \; \; \; \; \; \; R= \dfrac{P_fV_f}{n_fT_f} \]
Если заменить одно R на другое, то получится итоговое уравнение и общее уравнение газа:
\[ \dfrac{P_iV_i}{n_iT_i} = \dfrac {P_fV_f}{n_fT_f} \]
Стандартные условия
Если в каком-либо из законов переменная не указана, считать, что она задана. Для постоянной температуры, давления и количества:
Для постоянной температуры, давления и количества:
- Абсолютный ноль (Кельвин): 0 K = — 273,15 или С
T(K) = T( o C) + 273,15 (единица измерения температуры должна быть в Кельвинах)
2. Давление: 1 атмосфера (760 мм рт.ст.)
3. Количество: 1 моль = 22,4 л газа
4. В законе идеального газа газовая постоянная R = 8,3145 Дж · моль -1 · К -1
= 0,082057 л · атм·К — 1 · моль — 1
Уравнение Ван-дер-Ваальса для реальных газов 92} \) корректирует давление реального газа на действие сил притяжения между молекулами газа.
Точно так же, поскольку молекулы газа имеют объем, объем реального газа намного больше, чем у идеального газа, поправочный член \(1 -nb \) используется для корректировки объема, заполненного молекулами газа.
Практические задачи
- Если 4 л газа H 2 при 1,43 атм имеют стандартную температуру, а давление увеличилось в 2/3 раза, каков конечный объем H 2 газ? (Подсказка: закон Бойля)
- Если 1,25 л газа существует при температуре 35 o C и постоянном давлении 0,70 атм в цилиндрическом блоке, а объем необходимо умножить на коэффициент 3/5, какова новая температура газа? (Подсказка: закон Чарльза)
- Баллон с 4,00 г газообразного гелия имеет объем 500 мл.
 Когда температура и давление остаются постоянными. Каков будет новый объем гелия в баллоне, если добавить в баллон еще 4,00 г гелия? (Подсказка: Закон Авогадро)
Когда температура и давление остаются постоянными. Каков будет новый объем гелия в баллоне, если добавить в баллон еще 4,00 г гелия? (Подсказка: Закон Авогадро)
Решения
1. 2.40L
Для решения этого вопроса необходимо использовать закон Бойля: температура и количество газа постоянны и поэтому можно отложить в сторону, необходимы только:
- Начальное давление: 1,43 атм
- Начальный объем: 4 л
- Конечное давление: 1,43×1,67 = 2,39
- Последний том (неизвестно): V 2
Подставив эти значения в уравнение, вы получите:
В 2 = (1,43 атм x 4 л)/(2,39 атм) = 2,38 л
2, 184,89 К
90 023 Чтобы решить этот вопрос, вам нужно используйте закон Чарльза: Еще раз помните о ключевых переменных. Давление оставалось постоянным, и, поскольку количество газа не упоминается, мы предполагаем, что оно остается постоянным. В противном случае ключевые переменные:
В противном случае ключевые переменные:
- Начальный объем: 1,25 л
- Начальная температура: 35 o C + 273,15 = 308,15K
- Конечный объем: 1,25 л*3/5 = 0,75 л
- Конечная температура: T 2
Поскольку нам нужно решить для конечной температуры, вы можете изменить порядок Чарльза:
После подстановки чисел вы получите: T 2 = (308,15 K x 0,75 л) / (1,25 л) = 184,89 K
3. 1000 мл или 1 л
Используя закон Авогадро для решения этой задачи, вы можете преобразовать уравнение в \( V_2=\frac{n_1\centerdot V_2}{n_2} \). Однако вам нужно преобразовать граммы газообразного гелия в моли.
\[ n_1 = \frac{4,00г}{4,00г/моль} = \text{1 моль} \]
Аналогично, n 2 =2 моль
\[ V_2=\frac{n_2 \centerdot V_2}{n_1}\]
\[ =\frac{2 моль \centerdot 500 мл}{1 моль}\]
\[ = \text{1000 мл или 1 л } \]
Ссылки
- Petrucci, Ральф Х.
 Общая химия: принципы и современные приложения . 9-е изд. Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall, 2007. .
Общая химия: принципы и современные приложения . 9-е изд. Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall, 2007. . - Стейли, Деннис. Прентис Холл Химия . Бостон, Массачусетс: Пирсон Прентис Холл, 2007. .
Оландер, Дональд Р. «Глава 2 Уравнение состояния». Общая термодинамика . Бока-Ратон, Северо-Запад: CRC, 2008. Печать
.О’Коннелл, Джон П. и Дж. М. Хейл. «Свойства относительно идеальных газов». Термодинамика: основы приложений . Кембридж: Cambridge UP, 2005. Печать.
Гаре, Шакунтала. «Законы идеального газа для одного компонента». Закон идеального газа, энтальпия, теплоемкость, теплота растворения и смешения . Том. 4. Нью-Йорк, 1984. Печать. Ф.
Внешние ссылки
- http://en.Wikipedia.org/wiki/Gas_laws
- www.chem.queensu.ca/people/faculty/mombourquette/firstyrchem/GasLaws/index.
 htm
htm - vimeo.com/10588774
Законы о газе: обзор распространяется под лицензией CC BY-NC-SA 4.0 и был создан, изменен и/или курирован LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- № на стр.
- Теги

Газовые законы
Газовые законыНижеследующее является содержанием лекции 18. В этой лекции мы рассмотрим газовые законы: Шарля, Бойля, Авагадро и Гей-Люссака, а также законы идеального и комбинированного газа.
Законы свойств газа
Существует 4 общих закона, связывающих 4 основных характерных свойства газов друг с другом. Каждый закон назван по имени его первооткрывателя. Хотя важно понимать отношения, охватываемые каждым законом, знание отправителя не так важно и станет излишним после введения комбинированного закона о газах. Так что сконцентрируйтесь на понимании взаимосвязей, а не на запоминании имен.
Закон Чарльза- дает соотношение между объемом и температурой , если давление и количество газа поддерживаются постоянными :
1) Если увеличить температуру газа по шкале Кельвина, объем газа увеличится. (P, n постоянная)
2) Если температура газа по Кельвину уменьшается, объем газа уменьшается.(P, n постоянная)
Это означает, что объем газа прямо пропорционален его температуре по Кельвину. Подумайте об этом так: если вы увеличиваете объем газа и должны поддерживать постоянное давление, единственный способ добиться этого — повысить температуру газа.
Расчеты с использованием закона Чарльза включают изменение либо температуры (T 2 ), либо объема (V 2 ) от известного начального количества каждого из них (V 1 и T 1 ):
Закон Бойля — гласит, что объем данного количества газа при постоянной температуре изменяется обратно пропорционально приложенному давлению, когда температура и масса постоянны.
Уменьшение объема газа означает, что молекулы чаще ударяются о стенки, увеличивая давление, и, наоборот, если объем увеличивается, расстояние, которое молекулы должны пройти, чтобы удариться о стенки, увеличивается, и они реже ударяются о стенки, тем самым уменьшая давление. давление.
давление.
Как и закон Чарльза, закон Бойля можно использовать для определения текущего давления или объема газа, если известны начальные состояния и одно из изменений:
Закон Авагадро- Определяет соотношение между объемом и количеством газа в молях при постоянных давлении и температуре.
Если количество газа в контейнере увеличивается, объем увеличивается. Если количество газа в сосуде уменьшается, объем уменьшается. Это предполагает, конечно, что контейнер имеет расширяемые стенки.
Связь снова прямо пропорциональна, поэтому уравнение для расчетов
Закон Гей-Люссака гласит, что давление данного количества газа при постоянном объеме прямо пропорционально температуре Кельвина.
Если вы нагреваете газ, вы даете молекулам больше энергии, чтобы они двигались быстрее. Это означает большее количество ударов о стенки контейнера и увеличение давления. И наоборот, если вы охладите молекулы, они замедлятся, и давление уменьшится.
Это означает большее количество ударов о стенки контейнера и увеличение давления. И наоборот, если вы охладите молекулы, они замедлятся, и давление уменьшится.
Чтобы рассчитать изменение давления или температуры с помощью закона Гей-Люссака, уравнение выглядит следующим образом:
Чтобы немного поиграть с отношениями, попробуйте эту симуляцию.
Закон идеального газа:
Комбинация представленных выше законов порождает закон идеального газа:
Добавление константы пропорциональности, называемой идеальной или универсальной газовой постоянной (R), завершает уравнение.
Как видите, существует множество возможных единиц измерения константы. Единственная постоянная константа заключается в том, что температурная шкала во всем — КЕЛЬВИН.
При использовании закона идеального газа для расчета любого свойства газа вы должны сопоставлять единицы измерения с газовой постоянной, которую вы решили использовать, и вы всегда должны указывать свою температуру в градусах Кельвина.
Чтобы использовать уравнение, вам просто нужно определить, чего не хватает в вопросе, и перестроить уравнение, чтобы решить его.
Типичный вопрос был бы задан, поскольку 6,2 литра идеального газа содержатся при 3,0 атм и 37 °C. Сколько из этих молей газа присутствует?
Поскольку единицы газовой постоянной задаются с использованием атмосферы, молей и Кельвина, важно убедиться, что вы конвертируете значения, указанные в других шкалах температуры или давления. Для этой задачи переведите температуру в градусах Цельсия в К, используя уравнение:
.Т = °С + 273
Т = 37 °С + 273
Т = 310 К
Теперь вы можете подставить значения. Решите для количества родинок
н = ПВ/РТ
n = (3,0 атм x 6,2 л) / (0,08206 л атм/моль К x 310 К)
n = 0,75 моль
Вот несколько практических задач на использование закона идеального газа: Практика
Закон о комбинированном газе
Выше я сказал, что запоминание всех уравнений для каждого отдельного газового закона станет неактуальным после введения последующих законов.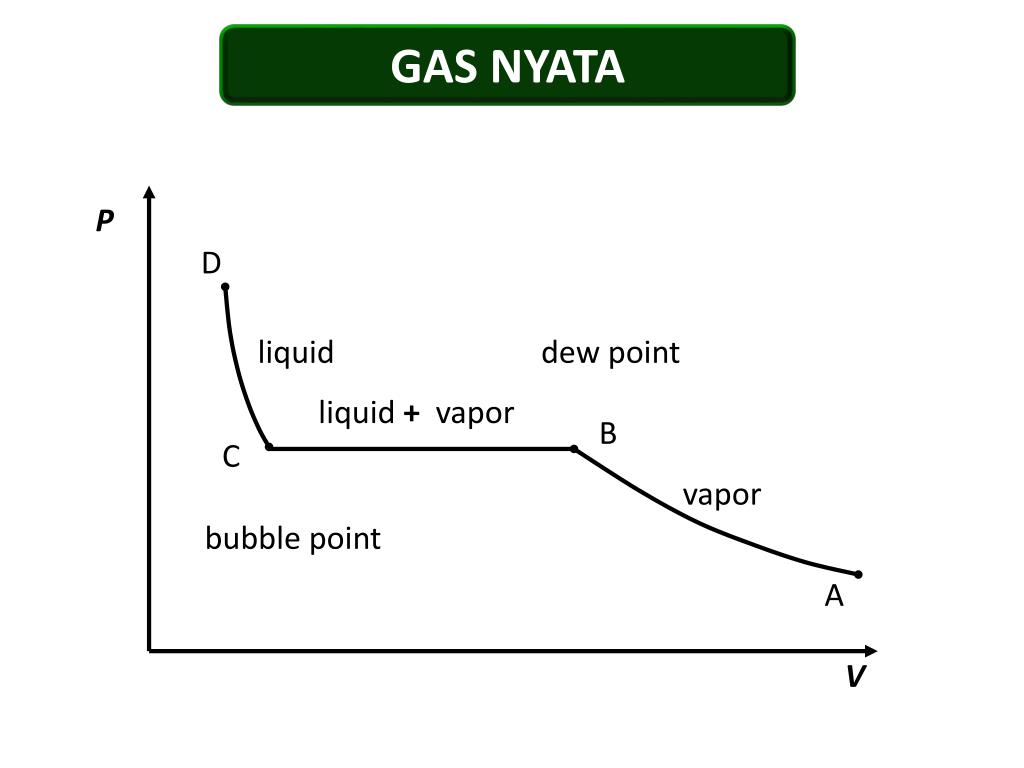 Закон, о котором я говорил, — это Закон о комбинированном газе:
Закон, о котором я говорил, — это Закон о комбинированном газе:
Комбинированный газовый закон позволяет вам получить любое из необходимых соотношений, комбинируя все изменяемые части в законе об идеальном газе: а именно: давление, температуру и объем. R и количество молей не фигурируют в уравнении, поскольку они обычно постоянны и, следовательно, сокращаются, поскольку они появляются в равных количествах в обеих частях уравнения.
Как видно выше, уравнение можно решить для любого из входящих в него параметров. Но что еще более важно, вы можете исключить из уравнения все, что останется постоянным.
Например, если в вопросе говорилось, что система при 1 атм и объеме 2 литра претерпела изменение на 3,5 литра, рассчитайте новое давление, вы можете просто исключить температуру из уравнения и получить:
P 2 = P 1 V 1 /V 2 = (1 атм)(2 л)/3,5 л) = 0,6 атм
Поскольку в вопросе никогда не упоминается температура, мы можем предположить, что она остается постоянной и поэтому не учитывается в расчетах.