«Свд» 7,62-мм снайперская винтовка драгунова техническое описание и инструкция по эксплуатации содержание

  • Введение

  • 1. Техническое описание

  • 1.1. Назначение винтовки

  • 1.2. Технические данные

  • 1.3. Состав винтовки

  • 1.4. Устройство и работа винтовки

  • 1.5. Устройство и работа прицела и его составных частей

  • 1.6. Принадлежность к винтовке

  • 1.7. Принадлежность к прицелу

  • 1.8. Тара и упаковка

  • 2. Инструкция по эксплуатации

  • 2.1. Общие указания

  • 2.2. Указания мер безопасности

  • 2.3. Подготовка снайперской винтовки и оптического прицела к стрельбе

  • 2.4. Приведение винтовки к нормальному бою и порядок работы с оптическим прицелом

  • 2. 5. Проверка технического состояния, характерные неисправности и методы их устранения

  • 2.6. Разборка и сборка винтовки

  • 2.7. Чистка и смазка

  • 2.8. Правила хранения и транспортирования

Введение

  Техническое описание и инструкция по эксплуатации 7,62-мм снайперской винтовки Драгунова (СВД) предназначены для изучения винтовок и оптических прицелов и поддержания их в постоянной боевой готовности.   В данном документе помещены технические характеристики и сведения об устройстве и принципе работы винтовки и оптического прицела, а также основные правила, необходимые для обеспечения правильной эксплуатации винтовки с прицелом и полного использования их технических возможностей.

1.Техническое описание

1.1. Назначение винтовки

  1.1.1. 7,62 мм снайперская винтовка Драгунова (индекс 6В1) является оружием снайпера и предназначена для уничтожения различных появляющихся, движущихся, открытых и маскированных одиночных целей (рис.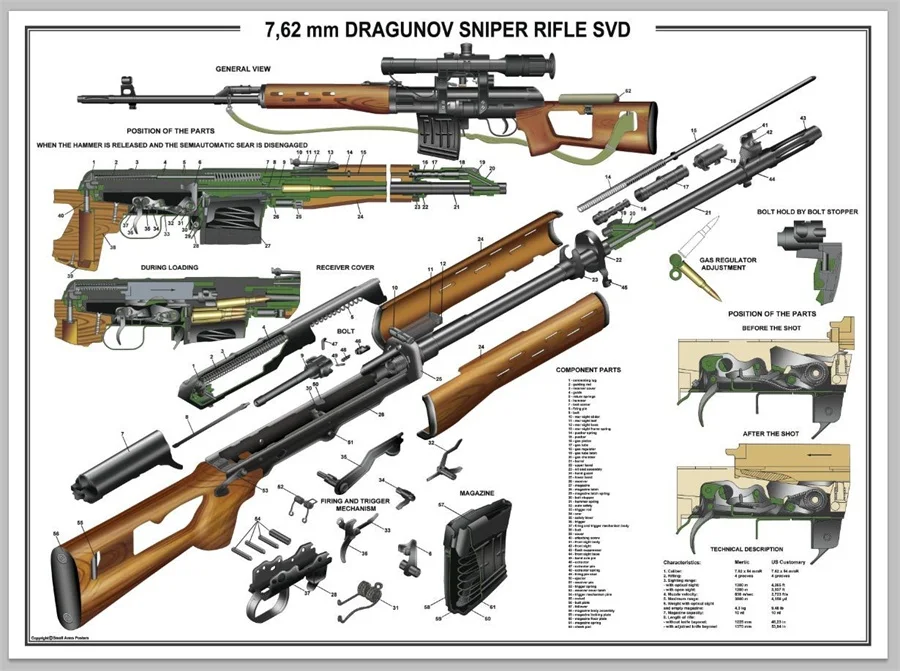

1).  Прицел снайперский оптический (индекс 6Ц1) служит для точного прицеливания из снайперской винтовки по различным целям.

Рис. 1. 7,62 мм снайперская винтовка Драгунова с оптическим прицелом и штыком-ножом:

1 — 7,62 мм снайперская винтовка Драгунова 6В1. сб.; 2 — прицел снайперский оптический 6Ц1. АЛЗ. 812. 000; 3 — штык-нож в сборе 6Х5 сб.

  1.1.2. Для стрельбы из снайперской винтовки применяются винтовочные патроны с обыкновенными, трассирующими и бронебойно-зажигательными пулями, а также снайперские патроны. Огонь из снайперской винтовки ведется одиночными выстрелами.  

1.1.3. Оптический прицел позволяет вести огонь ночью по инфракрасным источникам, а также при неблагоприятных условиях освещения, когда с открытым прицелом стрелять по целям затруднительно.   При наблюдении инфракрасных источников излучаемые источником инфракрасные лучи проходят через объектив прицела и воздействуют на экран, находящийся в фокальной плоскости объектива. В месте действия инфракрасных лучей на экране возникает свечение, дающее видимое изображение источника в виде круглого пятна зеленоватого цвета.

1.2. Технические данные

  1.2.1. Основные конструктивные баллистические характеристики винтовки, винтовочного патрона и конструктивные данные оптического прицела приведены в табл. 1.

Таблица 1

Наименование характеристики

Номинальная величина

1. Калибр, мм

7,62

2. Число нарезов

4

3. Прицельная дальность, м: с оптическим прицелом с открытым прицелом

1300 1200

4. Начальная скорость пули, м/с

830

5. Дальность полета пули, до которой сохраняется ее убойное действие, м

3800

6. Масса винтовки без штыка-ножа с оптическим прицелом, неснаряженным магазином и щекой, кг

4,3

7. Емкость магазина, патронов

10

8. Длина винтовки, мм: без штыка-ножа с примкнутым штыком-ножом

1220 1370

9. Масса патрона, г

21,8

10. Масса обыкновенной пули со стальным сердечником, г

9,6

11. Масса порохового заряда, г

3,1

12. Увеличение оптического прицела, крат.

4

13. Поле зрения прицела, градус

6

14. Диаметр зрачка выхода, мм

6

15. Удаление зрачка выхода, мм

68,2

16. Разрешающая способность, секунда,

12

17. Длина прицела с наглазником и выдвинутой блендой, мм

375

18. Ширина прицела, мм

70

19. Высота прицела, мм

132

20. Масса прицела, г

616

21. Масса прицела с комплектом ЗИП и чехлом, г

926

Война в Украине — оружие, которое помогает уничтожать российских оккупантов вблизи Бахмута (видео) — УНИАН

Украинские защитники называют немало преимуществ этого оружия, которое вытесняет советские образцы и помогает еще эффективнее уничтожать оккупантов.

ВСУ с помощью стрелкового оружия уничтожают врага / Скриншот

На Бахмутском направлении украинские защитники сдерживают российских захватчиков всеми возможными силами.  

Как рассказали в Минобороны Украины со ссылкой на сюжет журналистов военного телевидения, в этом воинам ВСУ, среди прочего, помогает стрелковое оружие.

В частности, это отечественная снайперская винтовка UAR-10 и штурмовая винтовка FN F2000.

Видео дня

Украинские защитники называют немало преимуществ этого оружия, которое вытесняет советские образцы и помогает еще эффективнее уничтожать оккупантов.

Так, отечественная снайперская винтовка UAR-10 имеет удобную конструкцию: может быть разобрана на две составные части, что позволяет уменьшить ее габариты и обеспечивает компактность при транспортировке. Прицельная дальность поражения — до тысячи двухсот метров, калибр — семь шестьдесят два миллиметра. Ствол винтовки консольно закреплен, чем достигается стабильность пристрелки. На верхней части ствольной коробки и на цевье выполнены направляющие типа Пикатини для установки прицельных приспособлений и других аксессуаров. Ударно-спусковой механизм допускает стрельбу только одиночными выстрелами, оптимизирован для точной стрельбы.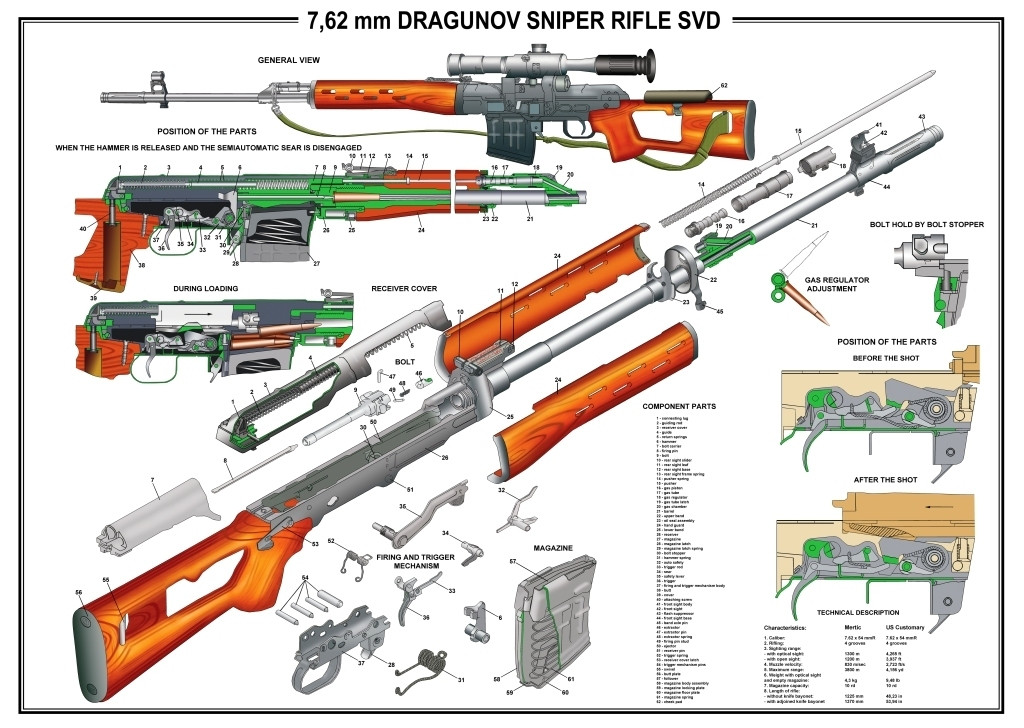 Эта винтовка заменила советскую СВД.

Читайте также:

«До этого я работал со СВД, она более привередлива, чем эта винтовка. С этой винтовкой работать проще. Нюанс в том, что СВД не такое чувствительное к загрязнениям как она. Ее надо чистить постоянно. Для того, чтобы ее разобрать нужно выдавить глазу два штифта, снять магазин, она разделяется на 2 части. Эта часть отделяется. Это казенник ствола и сам спусковой механизм. Отсюда вынимается сам затвор и, в принципе, для неполной чистки этого хватает», — поделился впечатлениями от работы оружия на военный позывной «Лесник».

Что касается штурмовой винтовки FN F2000, то она имеет довольно небольшой вес и длину. Скорострельность восемьсот пятьдесят выстрелов в минуту. Автоматика винтовки действует благодаря отводу пороховых газов, а замыкает ствол поворот замка. Корпус изготовлен из полимеров. Цевье можно легко снять, а на ее место установить дополнительный модуль.

Поэтому благодаря этому мощному стрелковому оружию украинские воины быстрее могут бороться с оккупантами РФ.

Журналисты показали оружие, которое помогает уничтожать оккупантов

Война в Украине: ситуация на Донбассе

Сейчас украинские войска продолжают освобождать Украину от российских захватчиков. Тяжелые бои продолжаются на Бахмутском направлении. В частности, западные эксперты отмечают, что на восточном участке фронта ситуация обостряется: россияне наступают сразу на Бахмутском и Авдеевском направлениях.

Глава Донецкой областной военной администрации Павел Кириленко сообщил, что линия фронта фактически полностью и круглосуточно под обстрелами, а город Бахмут очень сильно поврежден. Известно, что Россия стянула под Бахмут все возможные военные подразделения, которые строят линию обороны, потому что боятся наступления украинских сил. Враг пройти позиции не может, многочисленные потери у оккупантов фиксируются фактически ежедневно.

Ранее в Министерстве обороны Украины обнародовали видео с позиций украинских военных под Бахмутом Донецкой области.

Вас также могут заинтересовать новости:

  • Россиянам поставили задачу остановить продвижение ВСУ в Луганской области — Гайдай
  • СБУ задержала агента спецслужб РФ, который корректировал ракетные удары по Бахмуту
  • Битва за Донбасс обострилась, россияне наступают с удвоенной силой — ISW
Т\, $$

, где $v_i$ — это $i$-я -я главная компонента , или PC, а $\lambda_i$ — $i$-е собственное значение $S$, а также равно дисперсии данных вдоль $i$-го ПК.

Это разложение исходит из общей теоремы линейной алгебры, и некоторая работа должна быть проделана , чтобы мотивировать связь с PCA.

SVD — это общий способ понять матрицу с точки зрения пространства столбцов и строк. (Это способ переписать любую матрицу в терминах других матриц с интуитивно понятным отношением к пространству строк и столбцов.) Например, для матрицы $A = \left( \begin{array}{cc}1&2\\0&1\ end{array} \right)$ можно найти направления $u_i$ и $v_i$ в области и пронумеровать так, что 92 = (n-1) \lambda_i\,. $$

Общеизвестно, что левые сингулярные векторы $u_i$ охватывают пространство-столбец $X$. В этом конкретном случае $u_i$ дает нам масштабированную проекцию данных $X$ на направление $i$-й главной компоненты. Правые сингулярные векторы $v_i$ обычно охватывают пространство строк $X$, что дает нам набор ортонормированных векторов, которые охватывают данные так же, как PC.

В этой более длинной статье я расскажу о некоторых деталях и преимуществах взаимосвязи между PCA и SVD.

линейная алгебра. Почему Эндрю Нг предпочитает использовать SVD, а не EIG ковариационной матрицы для проведения PCA?

У @amoeba были отличные ответы на вопросы PCA, в том числе и на вопрос о связи SVD с PCA. Отвечая на ваш точный вопрос, я сделаю три пункта:

  • математически нет никакой разницы, вычисляете ли вы PCA непосредственно на матрице данных или на ее ковариационной матрице
  • разница исключительно из-за численной точности и сложности. Применение SVD непосредственно к матрице данных численно более стабильно, чем к ковариационной матрице
  • SVD можно применять к ковариационной матрице для выполнения PCA или получения собственных значений, на самом деле, это мой любимый метод решения собственных задач

Оказывается, SVD более устойчив, чем типичные процедуры разложения собственных значений, особенно для машинного обучения. В машинном обучении легко получить сильно коллинеарные регрессоры. СВД в этих случаях работает лучше.

Вот код Python для демонстрации. Я создал сильно коллинеарную матрицу данных, получил ее ковариационную матрицу и попытался получить собственные значения последней. SVD по-прежнему работает, а обычное собственное разложение в этом случае не работает.

 импортировать numpy как np
импортировать математику
из numpy импортировать linalg как LA
np.random.seed (1)
# создаем сильно коллинеарный ряд
Т = 1000
X = np.random.rand(T,2)
eps = 1e-11
X[:,1] = X[:,0] + eps*X[:,1]
C = np.cov (np.transpose (X))
print('Ков: ',С)
U, s, V = LA.svd(C)
print('SVD:',s)
w, v = LA.eig(C)
print('собственные значения: ',w)

Вывод:

 Cov: [[ 0,08311516 0,08311516]
 [0,08311516 0,08311516]]
СВД: [1.66230312e-01 5.66687522e-18]
собственные значения: [0,0,16623031]

Отвечая на комментарий Федерико Полони, вот код с тестированием стабильности SVD vs Eig на 1000 случайных выборках той же матрицы выше. Во многих случаях Eig показывает 0 маленькое собственное значение, что привело бы к сингулярности матрицы, а SVD здесь этого не делает. SVD примерно в два раза точнее при определении небольшого собственного значения, что может быть или не быть важным в зависимости от вашей проблемы.

 импортировать numpy как np
импортировать математику
из scipy.linalg импортировать toeplitz
из numpy импортировать linalg как LA
np.random.seed (1)
# создаем сильно коллинеарный ряд
Т = 100
р = 2
eps = 1e-8
m = 1000 # симуляций
err = np.ones((m,2)) # точность малого собственного значения
для j в диапазоне (м):
    u = np.random.rand(T,p)
    X = np.ones (u.shape)
    Х[:,0] = и[:,0]
    для i в диапазоне (1, p):
        X[:,i] = eps*u[:,i]+u[:,0]
    C = np.cov (np.transpose (X))
    U, s, V = LA.svd(C)
    w, v = LA.eig(C)
    # истинные собственные значения
    te = eps**2/2 * np.var(u[:,1])*(1-np.corrcoef(u,rowvar=False)[0,1]**2)
    ошибка[j,0] = s[p-1] - te
    err[j,1] = np.amin(w) - te
print('Ков: ',С)
print('SVD:',s)
print('собственные значения: ',w)
print('настоящие малые собственные числа: ',te)
акк = np.mean (np.abs (ошибка), ось = 0)
print("малое собственное значение, точность SVD, Eig: ",acc[0]/te,acc[1]/te)

Вывод:

 Cov: [[ 0,09189421 0,09189421]
 [0,09189421 0,09189421]]
СВД: [ 0,18378843 0.