2

Смазка Mobil Unirex N 2

Объем (л/кг): 180, 18, 16

Высокотемпературная смазка для подшипников.

Смазки UNIREX™ N 2 представляют собой премиальные продукты на основе литиевого комплекса, предназначенные для применения в подшипниках качения в условиях высоких температур. Данные универсальные смазки могут применяться в различном промышленном оборудовании; в частности, они рекомендованы для смазывания подшипников электродвигателей.

Продукт Unirex N 2 является смазкой класса 2 по NLGI, и предпочтительным способом ее применения в большинстве случаев является набивка вручную или с помощью смазочного шприца. Смазки UNIREX N 2 не предназначены для применения в условиях возможных задиров, когда требуются дополнительные антисварочные свойства.

Смазка UNIREX N 2 соответствует требованиям к смазочному материалу, регламентированным стандартами DIN 51825 — K2N — 20L и ISO L-XBDHA 2.

Оставить заявку

Технические характеристики

Смазки Unirex N 2 обладают превосходной эффективностью при высоких и низких температурах, водостойкостью, коррозионной стойкостью и продолжительным сроком службы при применении в подшипниках различных типов.

Особенности Преимущества и потенциальные выгоды
Превосходные рабочие показатели при высоких температурах. Загуститель на основе литиевого комплекса устойчив к размягчению / вытеканию из подшипников при температурах до 190°C.
Исключительный ресурс смазки Стендовые испытания подшипников в лаборатории показали превосходную эффективность смазывания при длительных режимах эксплуатации и температурах подшипников до 140°C.
Очень хорошие характеристики при низких температурах.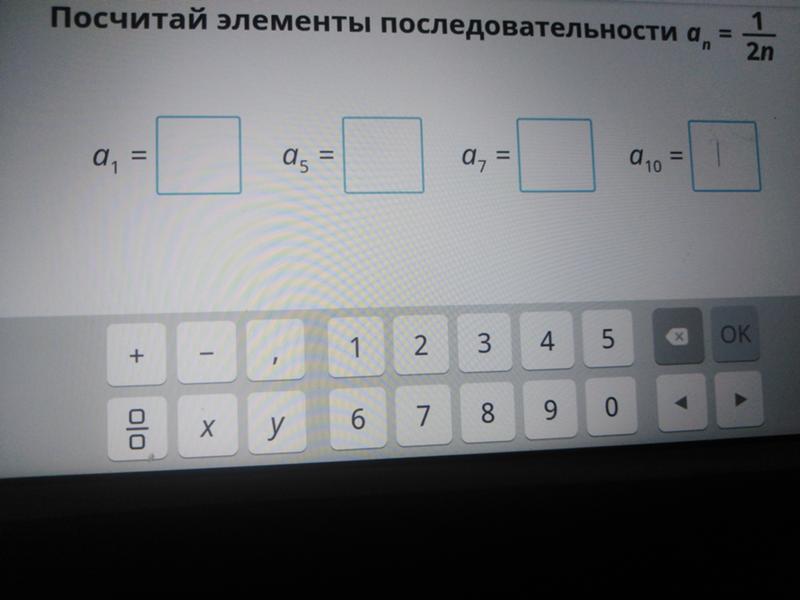 Требуемая мощность при пуске является низкой при температурах вплоть до -20°C. Соответствует требованиям DIN 51825 к крутящему моменту при низких температурах (-20°C).
Отличная механическая стабильность. Обладает превосходной стойкостью к размягчению при механической обработке.
Превосходная стойкость к воздействию воды и коррозии. Обладает стойкостью к вымыванию водой и защищает подшипники от коррозии.
Превосходные рабочие свойства в высокоскоростных узлах терния Высокая теплоотводящая способность обеспечивает превосходную эффективность работы в высокоскоростных шариковых радиальных подшипниках.

Продукт UNIREX N 2 является смазкой класса 2 по NLGI, и предпочтительным способом ее применения в большинстве случаев является набивка вручную или с помощью смазочного шприца. Смазка UNIREX N 2 рекомендована для смазывания электродвигателей. Она пригодна для двигателей по NEMA (Национальная ассоциация производителей электрооборудования) с классом изоляции A, B и F.

В большинстве случаев применение смазки UNIREX N 2 включает ручные методы нанесения. Несмотря на то, что продукт UNIREX N 2 пригоден для применения в автоматических централизованных системах, для оборудования, обслуживаемого такими системами, не будут актуальными такие свойства и преимущества смазки UNIREX N 2, как длительный срок службы, поскольку одной из функций автоматических систем является восполнение смазочного материала через относительно короткие интервалы времени.

  • DIN 51825: (2004-06) K2N-20L

Mobil Unirex N 2
Тип загустителя Литиевый комплекс
Класс по NLGI 2
Цвет, визуально Зеленый
Консистенция Мягкая, маслянистая
Температура каплепадения, ASTM D2265, °C
230
Вязкость базового масла, ASTM D 445, сСт при 40°C 115
Индекс вязкости базового масла, ASTM D 2270 95
Пенетрация перемешанной смазки после 60 ходов, ASTM D 217, мм/10 280
Изменение пенетрации перемешанной смазки после 100 тыс. рабочих ходов, ASTM D 217, мм/10 25
Отделение масла, ASTM D 6184, % масс. при 100°C / 30 ч 1,5
Испытание на коррозию EMCOR, ASTM D 6138, дистиллированная вода, класс
0,1
Вымывание водой при 79°C, ASTM D 1264, % масс. 3,7

По имеющейся информации, этот продукт не оказывает неблагоприятного воздействия на здоровье при правильном обращении и использовании. Дополнительная информация и рекомендации приведены в «Бюллетене данных по безопасному обращению с материалами». Эти Бюллетени предоставляются по запросу местным офисом, ответственным за продажи, или через Интернет. Этот продукт не должен применяться для других целей, кроме тех, для которых он предназначен. При утилизации использованного продукта, соблюдайте меры по защите окружающей среды.

Формула арифметического ряда — ChiliMath

Слово ряд подразумевает сумму . Мы можем преобразовать данную арифметическую последовательность в арифметическую серию, добавив члены последовательности. Пример ниже подчеркивает разницу между ними.

Последовательность против серии

Арифметическая последовательность (список):

\large{2,4,6,8,10,…}

Арифметическая последовательность (сумма):

\large{2 + 4 + 6 + 8 + 10…}

Обратите внимание, что в последовательности мы перечисляем термины, разделенные запятыми, а в сериях термины добавляются, как указано плюсом.

Таким образом, арифметическая последовательность представляет собой просто сумму членов арифметической последовательности . В частности, сумма первых \large\color{red}{n} членов арифметической последовательности называется частичной суммой . Частичная сумма обозначается символом \large{{S_n}}.

Ниже приведена общая форма формулы арифметического ряда. Лучше всего это работает, если в задаче заданы первый и последний члены.

Примечания:

▶︎ Формула арифметического ряда также известна как формула частичной суммы.

▶︎ Формула частичной суммы может быть описана словами как произведение среднего первого и последнего членов и общее количество членов в сумме.

▶︎ Формула арифметической последовательности включена в формулу частичной суммы. На самом деле это n-й член или последний член \large\color{blue}{a_n} в формуле.

▶︎ Ознакомиться с и формула арифметического ряда и формула арифметической последовательности (формула n-го члена), потому что они идут рука об руку при решении многих задач.

\Large{{S_n} = n\left( {{{{a_1} + \,{a_n}} \over 2}} \right)}

и

\large{{a_n} = {a_1} + \left( {n — 1} \right)d}

Прежде чем мы начнем работать с примерами, вы, возможно, помните, что я упоминал, что формула арифметической последовательности встроена в формулу арифметического ряда. Если мы заменим и расширим формула n-го члена в рамках формулы частичной суммы мы получим новую и полезную форму формулы арифметического ряда.

Ниже приведена альтернативная формула арифметического ряда. Учтите это, если последний член равен , а не .

Формула альтернативного арифметического ряда

где:

\large{{a_1}} – первый член

\large{{d}} – общая разность

\large{{n}} – число слагаемых в сумме

Примеры применения формулы арифметического ряда

Пример 1: Найдите сумму первых 100 натуральных чисел.

Это простая задача. Цель этой задачи — служить вводным примером. Это должно помочь вам быстро ознакомиться с формулой арифметического ряда. Как только вы поймете, как использовать формулу, вы сможете решать более сложные задачи, как вы увидите позже в этом уроке.

Напомним, что натуральные числа — это счетные числа. Мы можем записать конечную арифметическую последовательность как

1,2,3,4,…,100

и связанный с ней арифметический ряд как

1 + 2 + 3 + 4 + … + 100

Ясно, что первый член 1, последний член равен 100, и количество добавляемых членов также равно 100.

Подставьте значения в формулу, затем упростите, чтобы получить сумму.

Поскольку {a_1} = 1, {a_{100}} = 100 и n = 100, мы имеем

Таким образом, сумма первых 100 натуральных или счетных чисел равна 5050.

Если вы хотите больше попрактиковаться в нахождении суммы первых 200, 300, 400 и 500 натуральных чисел, вы можете использовать список частичных сумм натуральных чисел до 1000, который я создал в качестве ключа к ответу.

Пример 2: Найдите частичную сумму заданного арифметического ряда.

\large{7 + 12 + 17 + 22 + … + 187}

Если вы впервые решаете задачу такого типа, это может показаться вам немного сложным. Не то чтобы это сложно, а потому, что нужные вам значения не указаны явно. Это может сбить вас с толку, потому что вы даже не знаете, с чего начать. Однако, если у вас есть стратегия с самого начала, вы поймете, что эта проблема не так уж и плоха.

Нам нужно изучить данную серию. Определите ценности, которые важны и полезны для нас. Иногда, делая это таким образом, нам открывается следующий логический шаг.

Итак, это информация, которую мы собрали из сериала. Первый член равен 7. Так как 12-7=5, 17-12=5 и 22-17=5, то общая разность равна 5. Последний член равен 187. Это означает количество членов \large\color{ red}n, добавляемый в серию, отсутствует.

\большой{a_1} = 7

\large{d=5}

\large{a_n} = 187

\large{n = \,?}

Надеюсь, сейчас вы согласитесь со мной, что у нас нет другого выхода, кроме как использовать формула n-го члена , чтобы найти \large\color{red}n. Как только мы найдем значение для \large{n}, мы подставим его в формулу арифметического ряда вместе с первым и последним членами, чтобы найти сумму данного арифметического ряда.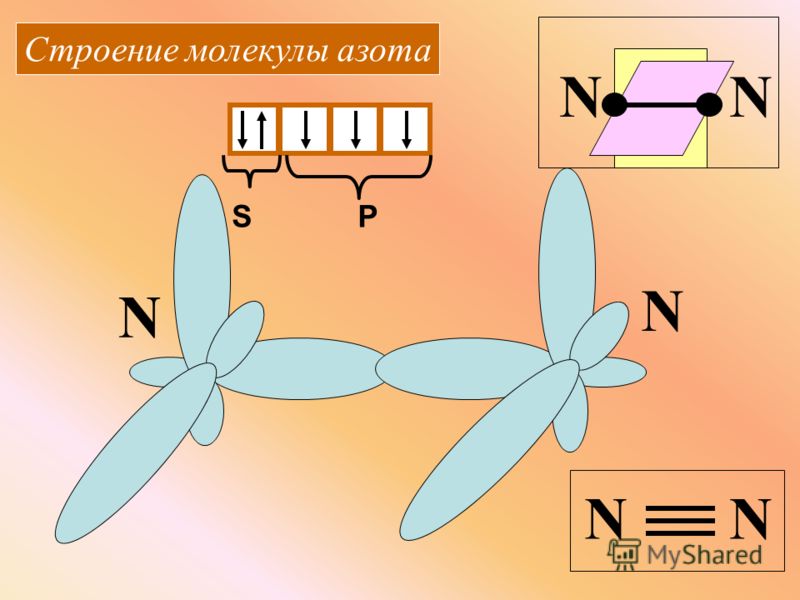

Теперь давайте найдем \large{n}, используя формулу n-го слагаемого.

Наконец, у нас есть все значения, необходимые для вычисления суммы заданного ряда: \large{n=37}, \large{a_1} = 7 и \large{a_n} = 187,

Пример 3: Найдите сумму первых больших членов арифметической прогрессии.

\large{12\,\,19\,\,26\,\,33\,…}

Стратегия аналогична примеру 2. Вместо нахождения количества членов \ большой\цвет{красный}n, мы будем использовать формулу n-го члена, чтобы найти 51-й член. Затем мы используем формулу арифметического ряда для вычисления суммы первых 51 членов последовательности.

Итак, какое значение мы можем извлечь из данной задачи?

Что ж, количество добавляемых терминов \large\color{red}n явно задано в задаче, которая равна n=51.

Теперь из арифметической последовательности легко определить первый член и общую разность. Первый член, очевидно, равен 12, а общая разность равна 7, поскольку 19 — 12 = 7, 26 — 19 = 7 и 33 — 26 = 7.

Итак, вот информация, которую мы собрали. Это означает, что n-й член — это то, что мы ищем.

\большой{a_1}=12

\большой{n=51}

\large{d=7}

\large{a_n}=\,?

Подставьте значения в формулу n-го члена , затем упростите, чтобы получить 51-й член.

Наконец мы можем найти сумму первых 51 слагаемых, потому что мы знаем количество слагаемых n=51, первое слагаемое {a_1}=7 и последнее слагаемое {a_n}=362.

Пример 4: 10-й член арифметической последовательности равен 17, а 30-й член равен -63. Чему равна 50-я частичная сумма \large{S_{50}} арифметической прогрессии?

Вот общая картина. Чтобы найти 50-ю частичную сумму, нам нужно знать первый член \large{a_1} и последний член \large{a_n}, который совпадает с 50-м членом. Очевидно, что в ряду будет 50 терминов, потому что мы суммируем термины с первого по 50-й член.

Чтобы найти первый член \large{a_1}, мы будем использовать формулу n-го члена вместе с данной информацией в задаче, чтобы сгенерировать систему уравнений, где неизвестными переменными являются первый член \large{a_1} и общая разница d.

\large{{a_n} = {a_1} + \left( {n — 1} \right)d}

Следовательно, мы имеем

  • 10-й член равен 17
  • 30-й член равен -63

Вот эту систему уравнений мы и собираемся решить. Мы можем найти значения первого члена \large{a_1} и общей разности \large{d}.

Мы решим эту систему уравнений, используя метод исключения. Мы вычтем уравнение №2 из уравнения №1, чтобы избавиться от \large{a_1}, тем самым изолировав \large{d}.

Это дает нам

Так как мы уже знаем значение общей разности \large{d}, мы можем легко найти первый член \large{a_1}. Выберите любое из двух уравнений, уравнение №1 или уравнение №2, подставьте значение \large{d}, затем решите для \large{a_1}. Мы выберем уравнение № 1, потому что с ним гораздо проще работать.

Зная первый член и общую разность последовательности, мы можем составить формулу, которая может определить любой член в последовательности.

Используя формулу, которую мы придумали, теперь мы можем найти 50-й член \large{{a_{50}}} в последовательности.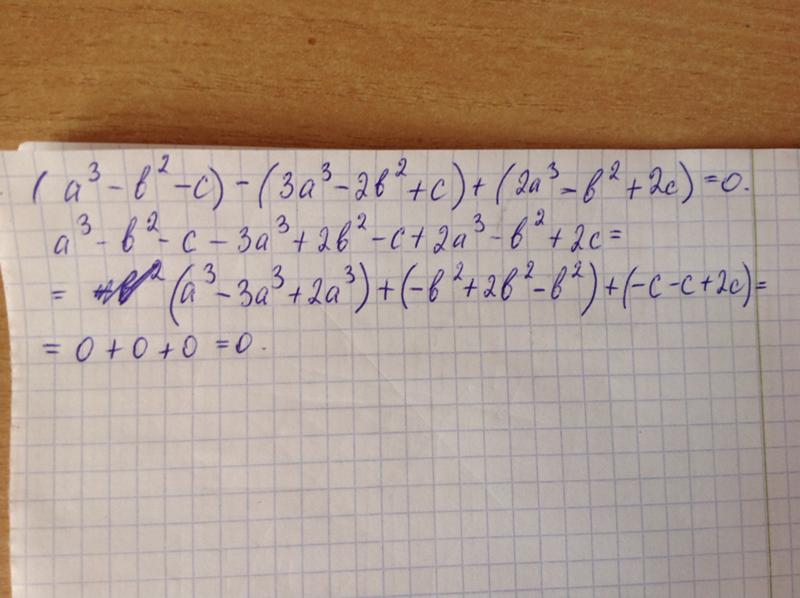

Наконец, у нас есть все, что нужно для вычисления 50-й частичной суммы с использованием формулы арифметического ряда.

Подставьте значения в формулу и упростите.

Пример 5: 10-й член арифметической прогрессии равен 23, а его 12-я частичная сумма равна 192. Найдите сумму первых 40 членов последовательности.

Чтобы найти первые 40 членов арифметической прогрессии, воспользуемся формулой основного арифметического ряда. Однако нам нужно указать недостающие значения в формуле, а именно первый член \large{{{a_1}}} и последний член \large{{{a_n}}}. Количество добавляемых членов \large{n} уже задано и равно 40.

Теперь построим систему уравнений, в которой неизвестными являются первый член \large{a{}_1} и общая разность \ большой {д}.

Первое уравнение исходит из данной информации, что \large{{a_{10}} = 23}. Подставьте значения в формулу n-го члена.

Второе уравнение исходит из данной информации, что \large{{S_{12}} = 192}. Подставьте значения в альтернативную формулу арифметического ряда.

Это система уравнений, которую мы будем решать методом исключения.

Умножьте уравнение №1 на -12.

Затем добавьте это к уравнению №2. Получаем {d=2}.

Найдя значение \large{d}, теперь мы можем найти значение \large{a{}_1}. Выберите любое из двух уравнений, подставьте значение \large{d}, затем найдите \large{a{}_1}. Мы будем использовать уравнение № 1, потому что это более простое уравнение.

Так как мы уже знаем значения \large{a{}_1} и \large{}_1}, теперь мы готовы написать общий член последовательности, который может найти любой член в последовательности.

Чтобы найти 40-й член , у нас есть

Наконец, у нас есть все необходимые значения, как показано ниже, для вычисления 40-й частичной суммы .

\large{n=40}

\large{{a_1} = 5}

\large{{{a_n} = 83}}

Подставьте значения в формулу арифметического ряда, затем упростите.

You might also be interested in:

Derivation of the Arithmetic Series Formula

Arithmetic Series Formula Practice Problems

Arithmetic Sequence Formula

Arithmetic Sequence Formula Practice Problems

Geometric Sequence Formula

Geometric Series Formula

Формула бесконечного геометрического ряда

Сумма первых n членов ряда

Горячая математика

Сумма членов последовательности называется ряд .

Если последовательность является арифметика или геометрический есть формулы для нахождения суммы первых н термины, обозначаемые С н , фактически не добавляя все термины.

(Обратите внимание, что последовательность не может быть ни арифметической, ни геометрической, и в этом случае вам нужно будет добавлять с помощью грубой силы или какой-либо другой стратегии.)

Сумма членов арифметической последовательности (арифметического ряда)

Чтобы найти сумму первых н члены арифметической прогрессии используют формулу,
С н «=» н ( а 1 + а 2 ) 2 ,
где н это количество терминов, а 1 является первым термином и а н это последний срок.

Пример 1:

Найдите сумму первых 20 члены арифметического ряда, если а 1 «=» 5 и а 20 «=» 62 .

С 20 «=» 20 ( 5 + 62 ) 2 С 20 «=» 670

Пример 2:

Найдите сумму первых 40 члены арифметической прогрессии
2 , 5 , 8 , 11 , 14 , ⋯

Сначала найдите 40 й срок:

а 40 «=» а 1 + ( н − 1 ) г «=» 2 + 39( 3 ) «=» 119

Затем найдите сумму:

С н «=» н ( а 1 + а н ) 2 С 40 «=» 40 ( 2 + 119) 2 «=» 2420

Пример 3:

Найдите сумму:

∑ к «=» 1 50 ( 3 к + 2 )

Первая находка а 1 и а 50 :

а 1 «=» 3 ( 1 ) + 2 «=» 5 а 20 «=» 3 ( 50 ) + 2 «=» 152

Затем найдите сумму:

С к «=» к ( а 1 + а к ) 2 С 50 «=» 50 ( 5 + 152 ) 2 «=» 3925

Сумма членов геометрического ряда (геометрического ряда)

Чтобы найти сумму первых н члены геометрической последовательности используют формулу,
С н «=» а 1 ( 1 − р н ) 1 − р , р ≠ 1 ,
где н это количество терминов, а 1 является первым термином и р это обыкновенное отношение .

Пример 4:

Найдите сумму первых 8 членов геометрического ряда, если а 1 «=» 1 и р «=» 2 .

С 8 «=» 1 ( 1 − 2 8 ) 1 − 2 «=» 255

Пример 5:

Находить С 10 геометрического ряда 24 + 12 + 6 + ⋯ .

Сначала найдите р .

р «=» р 2 р 1 «=» 12 24 «=» 1 2

Теперь найдите сумму:

С 10 «=» 24 ( 1 − ( 1 2 ) 10 ) 1 − 1 2 «=» 306964

Пример 6:

Оценивать.