Математика в деталях: how to математическая индукция
Начнем с того, что такое математическая индукция.
Математическая индукция – метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел, согласно Wikipedia. Говоря простыми словами, у нас есть какое-то математическое высказывание о натуральных числах, и мы хотим доказать/опровергнуть его истинность.
Разные источники дают разное определение натуральных чисел. В моем университете один профессор включает ноль во множество N, а по определению другого натуральные числа начинаются с единицы. Дело вкуса 😉 Но очень важно понять, с каким именно множеством вы работаете. Позже узнаете, почему.
Конечно, если наше математическое высказывание (формула) относится к маленькому множеству чисел, то гораздо легче просто высчитать ответ в уме или ввести данные в Wolfram – на этом всё, пускайте титры.
Например, вы, убивая время в интернете, где-то прочли, что сумма положительных натуральных чисел от 1 до n, то есть, 1+2+3+...+n, вычисляется по формуле n*(n+1)/2. Допустим, у вас проблемы с доверием, и вы хотите проверить, работает ли эта формула на самом деле, или это просто часть всемирного заговора?
Эту формулу можно применить к маленьким множествам, так как вы можете легко вычислить сумму чисел от 1 до 10, от 1 до 20, от 1 до 50, а если вас замучила бессонница, то попробуйте посчитать не овечек, а сумму чисел от 1 до 100. Помогает. Иногда.
Потом остается только подставить значения в формулу и сравнить.
Но если мы говорим о множестве с большим количеством элементов или о бесконечном множестве, то именно тут и пригодится индукция.
Проверка высказывания для наименьшего числа – это начало индукции.
Мы начинаем с базиса (база, base case) – нам дано наименьшее число, для которого нужно проверить истинность высказывания. Обычно это 1, но могут быть и другие варианты, которые обязательно указываются в условии. Например, можно начать с 4 или 5. Это не так важно. Но иногда этот базис не указывается эксплицитно. В этом случае вы начинаете с наименьшего числа вашего множества. Поэтому важно знать, с чего начать. Уточните, включается ноль в N или нет. В примерах в этой статье множество натуральных чисел начинается с единицы.
Затем мы утверждаем, что выражение истинно для любого n>=1. Мы не знаем этого наверняка, конечно. Но мы предполагаем, что если утверждение истинно для любого n, то оно будет верно и для n+1.
Это называется шагом индукции. А так как n – это любое число из множества N, то мы можем проверить математическое высказывание для очень-очень-очень больших чисел.
Итак, вернёмся к нашей формуле вычисления суммы чисел от 1 до n.
Начало индукции: проверяем, верна ли формула для n=1: n*(n+1)/2=> 1*(1+1)/2=1*(2)/2=1
Так как сумма чисел от 1 до 1 равна 1, то высказывание истинно для n=1.
Затем мы утверждаем, что математическое высказывание истинно для любого n>=1. То есть 1+2+3+...+n = n*(n+1)/2.
Переходим к шагу индукции – если высказывание верно для n, то оно истинно и для n + 1. 1+2+3+...+n + (n+1) = (n+1)(n+1 + 1)/2.
Левая часть уравнения – это сумма чисел от 1 до n+1.
Мы заменили все n в правой части на n+1, так как мы больше не рассматриваем n, а доказываем, что высказывание истинно именно для n+1.
Если вы помните, то сумма чисел от 1 до n вычисляется по формуле n*(n+1)/2. Поэтому часть выражения справа (а именно 1+2+3+...+n) можно заменить на n*(n+1)/2.
У нас остается n*(n+1)/2 + (n+1) = (n+1)(n+1 + 1)/2. Нам нужно доказать или опровергнуть равенство этих двух выражений.
Всё, что происходит дальше – это чистая алгебра. Нам надо всего лишь упростить эти выражения, так как немного трудно что-либо сказать об их равенстве, просто посмотрев на них. Даже если вы своими эльфийскими глазами можете рассмотреть, чему равны обе части, с вас всё равно потребуют формальное доказательство.
Немного упрощаем правую сторону:
n*(n+1)/2 + (n+1) = (n+1)(n+2)/2
Затем раскрываем скобки справа (умножаем n*(n+1)) и слева (умножаем (n+1)(n+2)).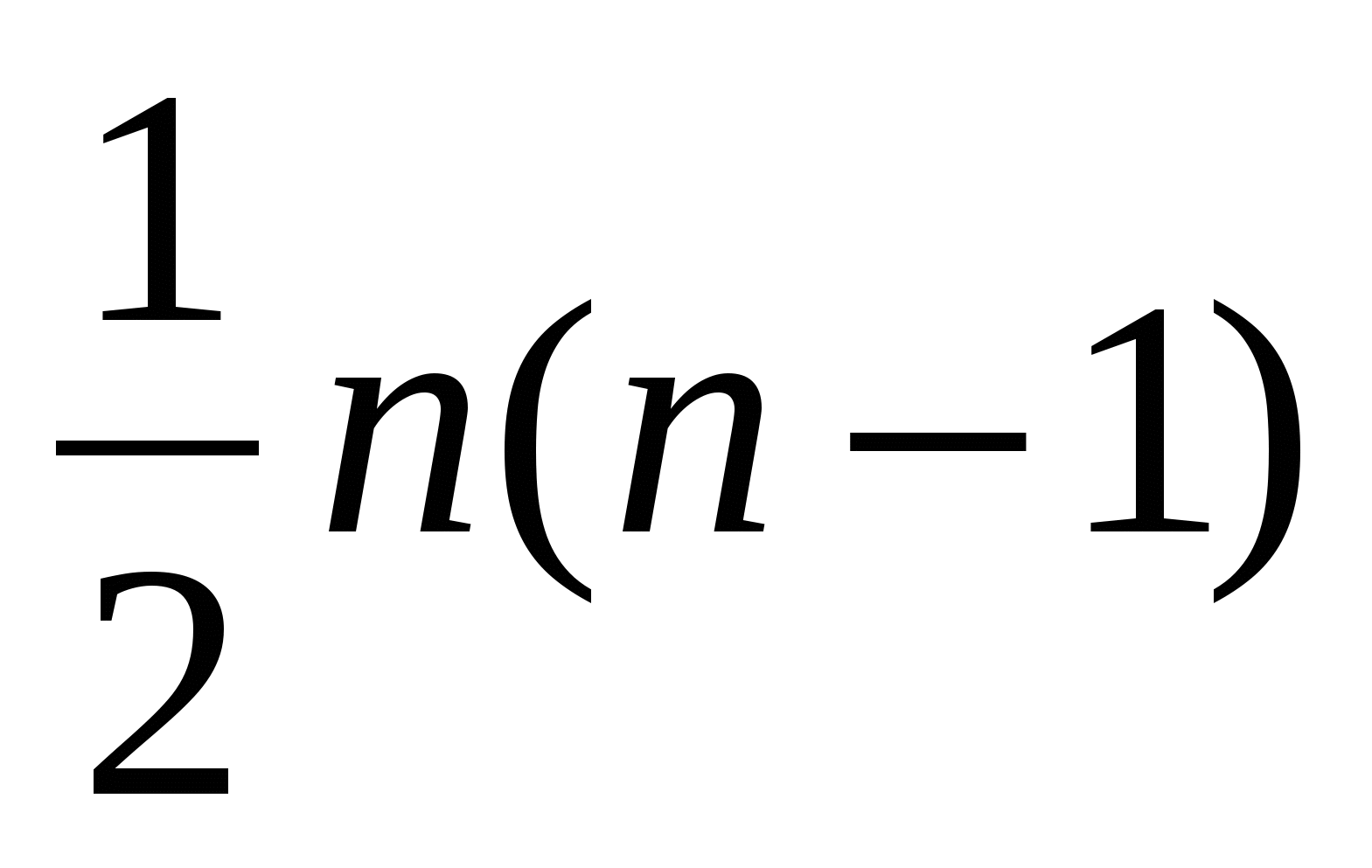
2 + 2n + 1
Правая и левая часть уравнения совпадают. Значит, математическое высказывание истинно.
Математическую индукцию еще сравнивают с эффектом домино. Если косточки домино выстроены в ряд, и какая-то упадёт, приложившись к следующей и опрокинув её, то та, в свою очередь, опрокинет следующую, и за ней последуют все остальные. А если мы опрокинем первую косточку, то упадёт весь ряд.
В индукции, если высказывание истинно для натурального числа, с которого мы начинаем, например, 8, то оно истинно для 9. Если оно истинно для 9, то оно верно для 10. И так далее. До бесконечности. Это мы и пытаемся доказать. Есть задачи, которые имею несколько базисов. Например, вам надо проверить какое-то высказывание для n=4, n=5, n=6 в начале индукции.
Попадаются и задачи, где база дана в рекурсивной форме.
Потренируйтесь на других примерах. Основным скилом для решения подобных задач является умение находить паттерны. Вы также должны понимать, что именно вы хотите доказать? Что описывает формула? Очень важно знать и уметь применять некоторые формулы, которые помогут вам упростить выражения. Например, те же самые формулы сокращённого умножения. Они очень часто встречаются в математической индукции. Очень многие допускают ошибки именно в конце, когда надо подключить свои знания алгебры.
Помните, что математическая индукция применяется только к высказываниям с натуральными числам. Ваш n не может равняться -10 или 8.5. Дискриминация по отношению к действительным и комплексным числам? Вполне может быть.
Для чего же это всё?
Во-первых, решая подобные задачи, вы развиваете логику и алгоритмическое мышление, что играет не последнюю роль в программировании.
Вы учитесь распознавать всякого рода паттерны.
Во-вторых, если вы внимательнее посмотрите на принцип математической индукции, вы заметите, что это чистейшая рекурсия. Предполагаю, что вы знакомы с рекурсией, если вы хотя бы немного программируете. Есть base case – условие завершения алгоритма. Также есть правило перехода. И чтобы проверить высказывание для n, нужно решить что-то для n-1, а потом с помощью алгебры дойти до n.
Рекурсию можно или любить, или люто ненавидеть. Но если ее понять и правильно использовать, она может сделать код элегантнее.
Схемы резервирования инженерных систем ЦОДЧто такое схема с N элементами в системе резервирования и как разобраться с, казалось бы, сложной таблицей Менделеева дата-центра? Прежде всего, необходимо сказать, что обозначение N происходит от английского слова «need», что в переводе обозначает «необходимость». Для системы резервирования этот символ N является обозначением необходимой нагрузки для эффективной работы оборудования. В одной системе, как правило, используются несколько N элементов. Их принцип работы зависит от схем, по которым они были воспроизведены. Существует несколько основных видов резервирования: N, N+1, 2N, 2N+1, 2(N+1), 3/2N. В зависимости от установленной схемы резервирования можно говорить об отказоустойчивости системы: чем система сложнее, тем она дороже и, соответственно, более устойчива к отказам и ошибкам. N. Отличительная черта такой схемы резервирования в том, что как такового резервирования в ней нет, а надежность зависит от каждого отдельного элемента N. При сбое в работе одного из них незамедлительно будет прекращена вся работа системы.
N+1 – схема с одним резервным элементом N. В системе N+1 резервный элемент остается незадействованным в работе до тех пор, пока в системе не произойдет сбой одного из основных элементов. В случае возникновения такого сбоя, резервный элемент примет на себя всю его нагрузку. Таким образом, система продолжит работать, но необходимость отключать всю систему для проведения ремонтных работ все еще возникнет. Для этого предусмотрены вариации: N+2, N+3 и т. 2
2N+1 — это параллельная система резервирования, схожая с системой 2N, но с одним дополнительным резервным элементом.
Таким образом, если ЦОД выйдет из строя или потребуется техническое обслуживание, то всю нагрузку можно перенести на параллельный блок, в то время как сам дата-центр продолжит работу без остановок. Схема 2(N+1) – это параллельная система резервирования с дополнительным элементом N, в которой резервный элемент дублируется, то есть это две полные системы по схеме N+1. При возникновении сбоя или необходимости технического обслуживания резервные элементы N остаются в любом случае, резервируются и ИБП, и системы охлаждения, ДГУ ждет своего часа на отдельной площадке. Эта система считается самой отказоустойчивой.
Схема 3/2N включает в себя все преимущества системы 2N, но такая система загружена на 2/3, а не на 50/50 как в системе 2N, соответственно и производительность у 3/2N будет намного выше, а счета за электричество – значительно меньше. При отказе одного из элементов минимальна вероятность потери нагрузки. Даже если выйдет из строя один из ИБП, то его нагрузку подхватит соседняя система. Как и в любой другой схеме, здесь возможны вариации: к примеру, если добавить четвертую группу ИБП, то схема уже будет называться 4/3 N.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
А для ЦОД необходима его бесперебойная работа, то есть системы резервирования прежде всего отвечают за отказоустойчивость источников бесперебойного питания и систем охлаждения.
Причина в том, что, когда один из элементов выходит из строя, его нагрузку перераспределить будет некуда. В результате такого сбоя данные могут быть безвозвратно утеряны, и это повлечет за собой, соответственно, материальные убытки. Эта схема уже давно не эксплуатируется как раз по причине того, что цена простоя всего ЦОД в случае неполадок слишком высока. По сути, при данной схеме зачастую отсутствует сам ИБП или генератор, а если даже они и есть, то представлены одномодульными системами.
д., в зависимости от требований уровня надежности и безопасности. Но стоит учитывать, что в этом варианте усложнение схемы может привести к большему простою.
23%
90%
000001сек
58%
9·10-18%
67сек но, конечно, я понятия не имею, как быть с таким суммированием, включающим более высокий порядок номера гармоники.
Вопрос 2: Как найти замкнутую форму для суммирования в (2)?
- интегрирование
- последовательности-и-ряды
- суммирование
- числа гармоник
$\endgroup$
2
$\begingroup$ 922+\frac12\ln2\G+2\Im\left\{\operatorname{Li_3}(1-i)\right\}$$
$\endgroup$
2
Скорости затухания внутренних приливов, оцененные с помощью усовершенствованного анализа взаимодействия волн
%PDF-1.4
%
1 0 объект
>
эндообъект
6 0 объект
>
эндообъект
2 0 объект
>
транслировать
doi:10.1175/JPO-D-17-0278.110.1175/JPO-D-17-0278.1 Скорость затухания внутренних приливов, оцененная с помощью улучшенного анализа взаимодействия волн http://dx.doi.org/10.
1175/JPO-D- 17-0278.12018-11-06false10.1175/JPO-D-17-0278.1
