Масса земли и радиус: Какой размер у планеты Земля? Радиус, площадь, масса и объем – SunPlanets.info

Физические основы механики

Закон всемирного тяготения позволяет установить масштабы расстояний и масс в Солнечной системе.

Радиус Земли можно найти с помощью геометрических измерений на ее поверхности. Первым это сделал Эратосфен (276–194 г. до н.э.), нашедший для радиуса Земли величину R₃ = 6 311 км. Эратосфен ошибся всего на 1 %: современное измерения для среднего радиуса Земли дают следующий результат: R₃ = 6 371,03 км. В действительности Земля не является шаром, более точная модель «фигуры Земли» такая: сплюснутый эллипсоид вращения со средним экваториальным радиусом (большая полуось эллипсоида)  км и полярным радиусом (меньшая ось эллипсоида)  км. Эксцентриситет этого эллипсоида вращения весьма невелик , поэтому в большинстве задач Землю, с вполне достаточной точностью, можно считать шаром.

Схема опыта Эратосфена показана на рис. 5.6. В полдень в день летнего солнцестояния в городе Сиен (ныне Асуан) Солнце находилось в зените, и предметы не отбрасывали тени. В тот же день и в то же время в городе Александрия, находившемся в 5 000 стадиях от Сиена Солнце отклонялось от зенита примерно на 7°. Это составляет примерно 1/50 полного круга (360°), откуда получается, что окружность Земли равна 250 000 стадий.

Зная длину меридиана, можно узнать каким «стадием» пользовался Эратосфен, поскольку в древности в ходу были следующие стадии:

• вавилонский = 194 м

• греческий = 178 м

o аттический = 177,6 м

o олимпийский = 192,27 м

• египетский = 172,5 м

o стадий системы фараонов = 209,4 м

• птолемеевский и римский = 185 м

• стадий (гхальва) ассиро-халдейско-персидской системы = 230,4 м

Рис. 5.6. Опыт Эратосфена по определению радиуса Земли

Как найти массу Земли? Каждое тело массой притягивается к ней с силой

где — масса Земли, а — расстояние от тела до центра Земли. С другой стороны, отношение силы к массе — это ускорение свободного падения (вращением Земли пренебрегаем):

Отсюда следует, что не зависит от массы и размеров тела и определяется исключительно параметрами Земли и расстоянием до нее. Вблизи поверхности Земли

и  = 9,81 м/с². Находим отсюда массу Земли:

Ближайшим к Земле небесным телом является Луна. Определим расстояние до Луны. Мы знаем, что период обращения Луны вокруг Земли равен = 27,32 сут = 27,32·86 400 = 2,36·10⁶ с. Центростремительное ускорение Луны

должно быть равно ускорению свободного падения на орбите Луны при = . Приравнивая и , находим:

Скорость Луны на орбите равна

Легко определить угловой диаметр Луны: большой палец, толщина которого примерно равна 1 см, закрывает при вытянутой руке (то есть на расстоянии примерно 1 м) ее диск. Отсюда

Более точные измерения дают для углового диаметра

Отсюда радиус Луны будет

Зная расстояние от Земли до Луны, с помощью геометрии можно определить расстояние от Земли до Солнца. Когда Луна находится в первой четверти, направления от нее в сторону Земли и в сторону Солнца составляют прямой угол (рис. 5.7).

Рис. 5.7. Геометрический метод определения расстояния от Земли до Солнца

Если в этот момент на Земле измерить угол между направлениями на Луну и Солнце, то расстояние до Солнца определится как

Угол оказывается близким к прямому: = 89°51′. Поэтому удобнее будет пользоваться дополнительным углом  = /2 – β = 9′ = 0,15° = 0,0026 рад. Тогда расстояние до Солнца будет равно

Это расстояние называется астрономической единицей (А или a.e., выше оно обозначено ). Более точно, A = 1,496·10¹¹ м.

Зная период обращения Земли вокруг Солнца = 1 год = 365,25 сут = 3,156·10⁷ с, находим скорость Земли на орбите:

Наконец, мы определим параметры Солнца. Видимый с Земли угловой диаметр Солнца примерно таков же, как и у Луны: φ = 32′ = 0,533° = 9,31·10^–3 рад. Отсюда находим радиус Солнца:

Массу Солнца получаем из закона всемирного тяготения: центростремительное ускорение Земли на орбите

должно быть равно ускорению свободного падения Земли на Солнце

Приравнивая и , получаем:

В этом выражении мы видим знакомую по третьему закону Кеплера комбинацию: отношение куба расстояния от планеты до Солнца к квадрату периода обращения. У всех планет это отношение одинаково, так как они вращаются вокруг одной и той же звезды.

Орбитальную скорость Земли можно также записать в виде

Это выражение справедливо для любой планеты при соответствующем изменении радиуса орбиты .

Приведенные оценки показывают, как много можно узнать о мире, наблюдая его из удобного кресла и … понимая законы природы.

Дополнительная информация

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 41–42 (§ 4, задача 4): о скорости движения тени Луны по поверхности Земли во время полного солнечного затмения.

http://school-collection.edu.ru/catalog/res/e6609a18-088c-4979-83f0-faeeeef9faa1/?sort=order&from=ffb3b711-8f44-408c-aea4-a29842431067&&rubric_id%5B%5D=110200&rubric_id%5B%5D=110201 — Соросовский образовательный журнал, 1998 г., № 2 — анимация «Вращение Земли вокруг Солнца. День, ночь, времена года, фазы Луны».

http://www.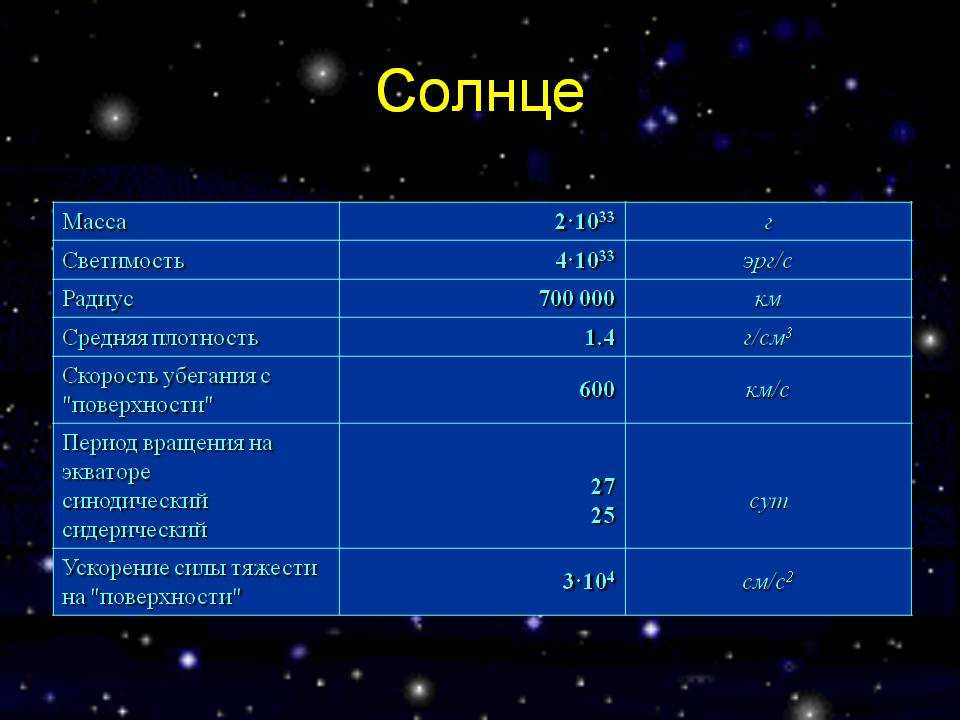 somit.ru/fisika7_1.html — анимация, демонстрирующая причину смены дня и ночи на Земле и движение Луны.

Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы «Кинематика», «Динамика, «Равновесие тел» и «Законы сохранения в механике». Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

Как была определена масса Земли?

АстрономияПланетыНаука

Расчет

Как определяется масса Земли? Ньютон, Галилей, Генри Кавендиш и Эратосфен внесли свой вклад в этот удивительный расчет.

Этот расчет выполняется с использованием Закон всемирного тяготения Ньютона , формулирующий силу притяжения (силу гравитации), с которой две массы действуют друг на друга:

F=ГмМ/р ²

• В уравнении Ньютона F — гравитационная сила, G — константа пропорциональности, M и m — две массы, действующие на силы, r — расстояние между двумя объектами.
• Гс было рассчитано Генри Кавендишем в 1798 году и составило 6,67 x 10-11 м3/(кг сек2).
• Также необходим второй закон движения Ньютона, F=ma , где F — сила, приложенная к объекту, m — масса объекта, а — его ускорение под действием силы.
• Галилей определил, что ускорение под действием силы тяжести Земли является постоянной величиной, равной 9,8 м/сек2 вблизи поверхности Земли.
• Наконец, вам нужно знать радиус Земли; это впервые было вычислено греком Эратосфеном тысячи лет назад (путем сравнения теней в колодцах во время летнего солнцестояния около 230 г. до н. э.).

Расчет массы Земли

1. F ​​= GmM/r2 = ma , где F — сила тяжести, G — гравитационная постоянная, M — масса Земли, r — радиус Земли, m — масса другого объекта (у поверхности Земли).
2. GM/r2= a (М исключено.) Теперь найдите М, массу Земли.
3. М = ar2/G , где а = 9,8 м/с2, r = 6,4 х 106 м, G = 6,67 х 10-11 м3/(кг с2).
4. М = 9,8 х (6,4 х 106)2/(6,67 х 10-11) = 6,0 х 1024 кг

Люди, стоящие за расчетами

КЭВЕНДИШ, ГЕНРИ

Генри Кавендиш (1731–1810) — английский химик и физик. Кавендиш открыл, что газообразный водород представляет собой вещество, отличное от обычного воздуха (компоненты которого он проанализировал), описал состав воды (водород и кислород) и другие важные работы. Кавендиш был первым, кто определил гравитационную постоянную Ньютона и точно измерил массу и плотность Земли.

ЭРАТОСФЕН

Эратосфен (276-194 гг. до н.э.) был греческим ученым, который первым определил окружность Земли. Он сравнил полуденную тень в середине лета в глубоких колодцах Сиены (ныне Асуан на Ниле в Египте) и Александрии. Он правильно предположил, что солнечные лучи практически параллельны (поскольку Солнце так далеко). Зная расстояние между двумя точками, он вычислил окружность Земли в 250 000 стадий. Точно неизвестно, как долго длится стасия, поэтому его точность сомнительна. Он также точно измерил наклон земной оси и расстояние до Солнца и Луны и разработал метод определения простых чисел до заданного числа (решето Эратосфена). Эратосфен внес большой вклад в науку и искусство во многих областях, включая географию, математику, астрономию, хронографию (календари), музыку и литературу. Эратосфен был блестящим разносторонним ученым; хотя он и не был лучшим специалистом по какой-либо теме, он хорошо разбирался во всех предметах, и поэтому получил прозвище «Бета» (что является второй буквой греческого алфавита).

ГАЛИЛЕЙ, ГАЛИЛЕО

Галилео Галилей (1564—1642) — итальянский математик, астроном и физик. Он был первым человеком, который использовал телескоп для наблюдения за небом (в 1609 году). Галилей открыл четыре спутника Юпитера, наблюдал фазы Венеры, изучал солнечные пятна и открыл многие другие важные явления. После публикации многих открытий, которые он сделал с помощью своего телескопа, включая движение Земли вокруг Солнца (система Коперника), Галилей был обвинен инквизицией в ереси (в 1633 году).

НЬЮТОН, ИСААК

Исаак Ньютон (1642-1727) — английский математик и физик, который изобрел исчисление (одновременно, но независимо от Лейбница), сформулировал законы гравитации и механики, исследовал природу света (открыл, что солнечный свет состоит из света разных цветов ).

Земля имеет массу 5,97 × 1024 кг, радиус 6,37 × 106 м. Земля…

Земля имеет массу 5,97 × 1024 кг, радиус 6,37 × 106 м. Земля… | Каналы для Pearson+

Последние каналы

• Физика

Химия

• Общая химия
• Органическая химия
• Химия 9 GOB Аналитическая химия

  8 8

• Биохимия

Биология

• Общая биология
• Микробиология
• Анатомия и физиология
• Генетика
• Клеточная биология

Математика

• Колледж Алгебра
• Тригонометрия
• Предварительное исчисление

Физика

• Физика

Бизнес

• Микроэкономика
• Макроэкономика
Социальные науки2
• Финансовый учет
• Финансовый учет8
  • Психология

  Начните печатать, затем используйте стрелки вверх и вниз для выбора вариант из списка.

  Физика16. Угловой моментУгловой момент массы точки

  Множественный выбор

  Земля имеет массу 5,97×10 ²⁴ кг, радиус 6,37×10 ⁶ м. Расстояние от Земли до Солнца составляет 1,5 × 10 ¹¹ м. Вычислите его угловой момент, когда он вращается вокруг себя. Рассматривайте Землю как твердую сферу с равномерным распределением массы.

  БОНУС 1: Рассматривая Землю как точечную массу, рассчитайте ее угловой момент, когда она вращается вокруг Солнца.

  БОНУС 2: Имеет ли Земля линейный импульс, когда она вращается вокруг (i) самой себя; (ii) Солнце?

  L _E,E = 4,23×10 ³³ кг•м ² /с

  L _E,E = 7,05×10 ³³ кг•м ² /с

  L ^{E,E,E,69 022 34} кг • M ² /S

  L _{E, E} = 2,68 × 10 ³⁴ кг • M ² /S

  Следующие

  Master угловой моментальный момент из точечной массы с прикусом.