Движение луны вокруг земли схема. Движение луны вокруг земли
Можно сказать, что на первый взгляд Луна просто движется вокруг планеты Земля с определенной скоростью и по определенной орбите.
В реальности это очень сложный трудноописуемый с научной точки зрения процесс движения космического тела, протекающий под воздействием множества различных факторов. Таких, например как, форма Земли, если мы помним из школьной программы, она немного сплюснута, а так же очень сильно влияет то, что например, Солнце притягивает ее в 2,2 раза сильнее, чем наша родная планета.
Снимки космического аппарата Deep Impact последовательность перемещения Луны
При этом производя точные расчеты движения, необходимо так же учитывать, что посредством приливного взаимодействия Земля передает Луне момент импульса вращения, тем самым создавая силу, заставляющую ее отдаляться от себя. При этом гравитационное взаимодействие данных космических тел является не постоянным и с увеличением расстояния оно уменьшается, приводя к уменьшению и скорость удаления Луны.
Почему она светится?
Вы не задавались вопросом, почему иногда мы видим только часть Луны? Или почему она светится? Давайте разберёмся в этом! Спутник отражает лишь 7% солнечного света падающего на нее. Это происходит, потому что в период бурной активности Солнца лишь отдельные участки ее поверхности способны поглощать и накапливать солнечную энергию, а после слабо излучать ее.
Пепельный свет — отраженный свет от Земли
Сама по себе она не может светиться, а способна лишь отражать свет Солнца. Поэтому мы видим только ту ее часть, которую ранее осветило Солнце. Данный спутник движется по определенной орбите вокруг нашей планеты и угол между ним, Солнцем и Землей постоянно меняется, в результате мы и видим различные фазы Луны.
Инфографика «Фазы Луны»
Время между новолуниями составляет 28,5 дня. То, что один месяц длиннее другого можно объяснить движением Земли вокруг Солнца, то есть когда спутник делает полный оборот вокруг Земли, сама планета в этот момент продвигается на 1/13 часть вокруг своей орбиты.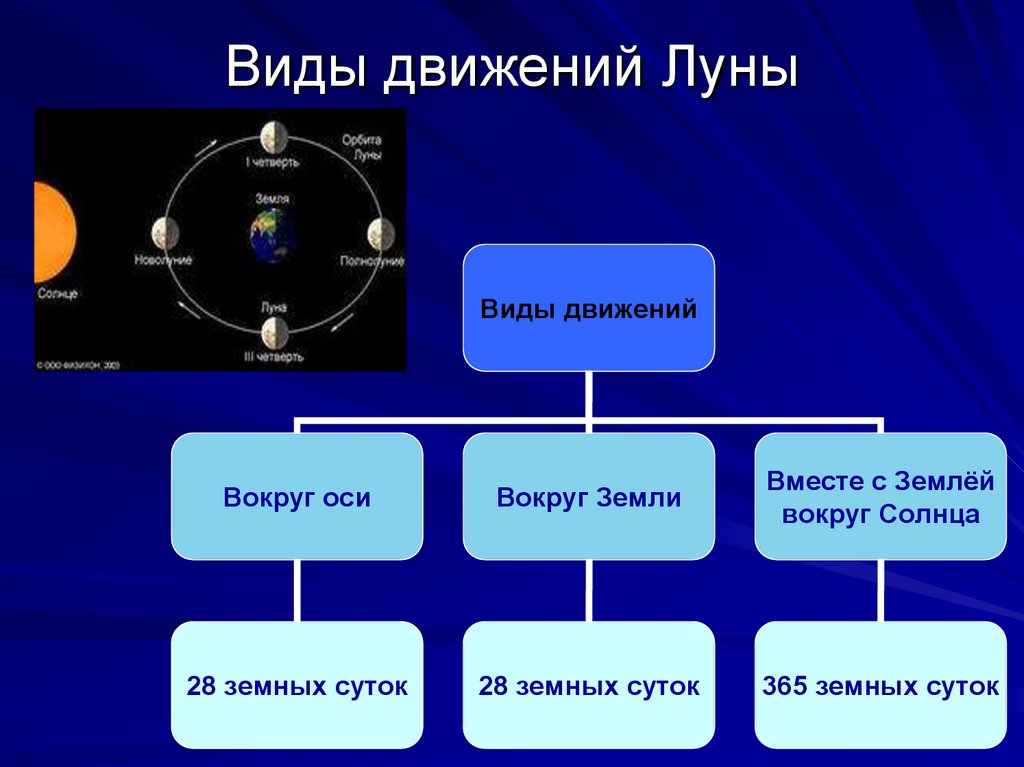
Несмотря на то, что она постоянно вращается вокруг своей оси, она всегда смотрит на Землю одной и той же стороной, это значит, что вращение, которое она совершает вокруг собственной оси и вокруг самой планеты синхронно. Эта синхронность вызвана приливами.
Обратная сторона
Обратная сторона
Наш спутник вращается вокруг собственной оси равномерно, а вокруг Земли согласно определенному закону, суть которого состоит в следующем: данное движение неравномерно — вблизи перигея оно быстрее, а вот вблизи апогея чуть медленнее.
Иногда возникает возможность взглянуть на оборотную сторону Луны, если вы находитесь на востоке или, например на западе. Это явление носит название оптической либрацией по долготе, существует еще и оптическая либрация по широте. Она возникает из-за наклона лунной оси относительно Земли, и наблюдать это можно на юге и севере.
Естественным спутником Земли является Луна — несветящееся тело, которое отражает солнечный свет.
Изучение Луны началось в 1959 г., когда советский аппарат «Луна-2» впервые сел на Луну, а с аппарата «Луна-3» впервые были сделаны из космоса снимки обратной стороны Луны.
В 1966 г. аппарат «Луна-9» совершил посадку на Луну и установил прочную структуру грунта.
Первыми, кто побывал на Луне, стали американцы Нейл Армстронг и Эдвин Олдрин. Это произошло 21 июля 1969 г. Советские ученые для дальнейшего изучения Луны предпочли использовать автоматические аппараты — луноходы.
Общие характеристики Луны
Средняя удаленность от Земли, км | |
|
|
|
|
Среднее расстояние между центрами Земли и Луны, км | |
Наклон орбиты к плоскости ее орбиты | |
Средняя орбитальная скорость |
|
Средний радиус Луны, км | |
Масса, кг | |
Экваториальный радиус, км | |
Полярный радиус, км | |
Средняя плотность, г/см 3 | |
Наклон к экватору, град. |
Масса Луны составляет 1/81 массы Земли. Положение Луны на орбите соответствует той или иной фазе (рис. 1).
Рис. 1. Фазы Луны
Фазы Луны — различные положения относительно Солнца — новолуние, первая четверть, полнолуние и последняя четверть. В полнолуние виден освещенный диск Луны, так как Солнце и Луна находятся на противоположных сторонах от Земли. В новолуние Луна находится на стороне Солнца, поэтому сторона Луны, обращенная к Земле, не освещается.
К Земле Луна обращена всегда одной стороной.
Линию, которая отделяет освещенную часть Луны от неосвещенной, называют терминатором.
В первой четверти Луна видна на угловом расстоянии 90″ от Солнца, и солнечные лучи освещают лишь правую половину обращенной к нам Луны. В остальных фазах Луна видна нам в виде серпа. Поэтому, чтобы отличить растущую Луну от старой, надо помнить: старая Луна напоминает букву «С», а если Луна растущая, то можно мысленно перед Луной провести вертикальную линию и получится буква «Р».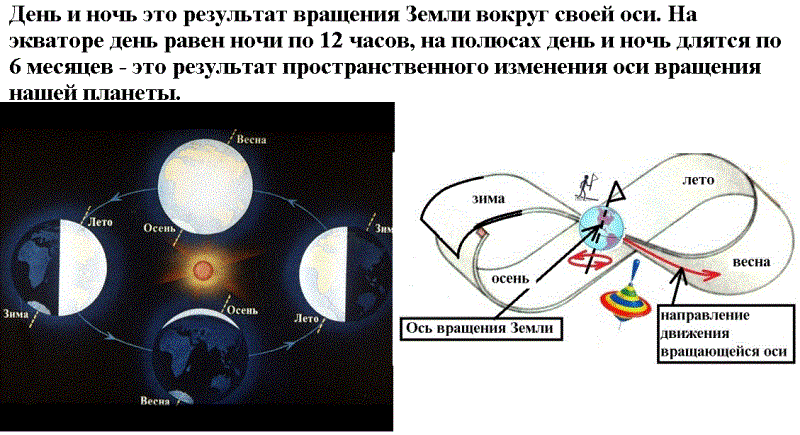
Из-за близости Луны к Земле и ее большой массы они образуют систему «Земля-Луна». Луна и Земля вращаются вокруг своих осей в одну сторону. Плоскость орбиты Луны наклонена к плоскости орбиты Земли под углом 5°9″.
Места пересечения орбит Земли и Луны называют узлами лунной орбиты.
Сидерический (от лат. сидерис — звезда) месяц — это период вращения Земли вокруг своей оси и одинакового положения Луны на небесной сфере по отношению к звездам. Он составляет 27,3 земных суток.
Синодическим (от греч. синод — соединение) месяцем называют период полной смены лунных фаз, т. е. период возвращения Луны в первоначальное положение относительно Луны и Солнца (например, от новолуния до новолуния). Он составляет в среднем 29,5 земных суток. Синодический месяц на двое суток длиннее сидерического, так как Земля и Луна вращаются вокруг своих осей в одну сторону.
Сила тяжести на Луне в 6 раз меньше силы тяжести на Земле.
Рельеф спутника Земли хорошо изучен. Видимые темные участки на поверхности Луны названы «морями» — это обширные безводные низменные равнины (самая крупная — «Оксан Бурь»), а светлые участки — «материками» — это гористые, возвышенные участки. Основные же планетарные структуры лунной поверхности — кольцевые кратеры диаметром до 20-30 км и многокольцевые цирки диаметром от 200 до 1000 км.
Видимые темные участки на поверхности Луны названы «морями» — это обширные безводные низменные равнины (самая крупная — «Оксан Бурь»), а светлые участки — «материками» — это гористые, возвышенные участки. Основные же планетарные структуры лунной поверхности — кольцевые кратеры диаметром до 20-30 км и многокольцевые цирки диаметром от 200 до 1000 км.
Происхождение у кольцевых структур различное: метеоритное, вулканическое и ударно-взрывное. Кроме этого, на поверхности Луны имеются трещины, сдвиги, купола и системы разломов.
Исследования космических аппаратов «Луна-16», «Луна-20», «Луна-24» показали, что поверхностные обломочные породы Луны сходны с земными магматическими породами — базальтами.
Значение Луны в жизни Земли
Хотя масса Луны в 27 млн раз меньше массы Солнца, она в 374 раза ближе к Земле и оказывает на нес сильное влияние, вызывая поднятия воды (приливы) в одних местах и отливы в других. Это происходит каждые 12 ч 25 мин, так как Луна делает полный оборот вокруг Земли за 24 ч 50 мин.
Из-за гравитационного воздействия Луны и Солнца на Землю возникают приливы и отливы (рис. 2).
Рис. 2. Схема возникновения приливов и отливов на Земле
Наиболее отчетливы и важны по своим следствиям прилив- но-отливные явления в волной оболочке. Они представляют собой периодические подъемы и опускания уровня океанов и морей, вызываемые силами притяжения Луны и Солнца (в 2,2 раза меньше лунной).
В атмосфере приливно-отливные явления проявляются в полусуточных изменениях атмосферного давления, а в земной коре — в деформации твердого вещества Земли.
На Земле наблюдаются 2 прилива в ближайшей и удаленной от Луны точке и 2 отлива в точках, находящихся на угловом расстоянии 90° от линии Луна — Земля. Выделяют сигизийные приливы, которые возникают в новолуние и полнолуние и квадратурные — в первой и последней четверти.
В открытом океане приливно-отливные явления невелики. Колебания уровня воды достигает 0,5-1 м. Во внутренних морях (Черное, Балтийское и др. ) они почти не ощущаются. Однако в зависимости от географической широты и очертаний береговой линии материков (особенно в узких заливах) вода во время приливов может подниматься до 18 м (залив Фанди в Атлантическом океане у берегов Северной Америки), 13 м на западном побережье Охотского моря. При этом образуются приливно-отливные течения.
) они почти не ощущаются. Однако в зависимости от географической широты и очертаний береговой линии материков (особенно в узких заливах) вода во время приливов может подниматься до 18 м (залив Фанди в Атлантическом океане у берегов Северной Америки), 13 м на западном побережье Охотского моря. При этом образуются приливно-отливные течения.
Основное значение приливных волн заключается в том, что, перемешаясь с востока на запад вслед за видимым движением Луны, они тормозят осевое вращение Земли и удлиняют сутки, изменяют фигуру Земли с помощью уменьшения полярного сжатия, вызывают пульсацию оболочек Земли, вертикальные смещения земной поверхности, полусуточные изменения атмосферного давления, изменяют условия органической жизни в прибрежных частях Мирового океана и, наконец, влияют на хозяйственную деятельность приморских стран. В целый ряд портов морские суда могут заходить только во время прилива.
Через определенный промежуток времени на Земле повторяются солнечные и лунные затмения. Увидеть их можно, когда Солнце, Земля и Луна находятся на одной линии.
Увидеть их можно, когда Солнце, Земля и Луна находятся на одной линии.
Затмение — астрономическая ситуация, при которой одно небесное тело заслоняет свет от другого небесного тела.
Солнечное затмение происходит, когда Луна попадает между наблюдателем и Солнцем и загораживает его. Поскольку Луна перед затмением обращена к нам неосвещенной стороной, перед затмением всегда бывает новолуние, т. е. Луна не видна. Создается впечатление, что Солнце закрывается черным диском; наблюдающий с Земли видит это явление как солнечное затмение (рис. 3).
Рис. 3. Солнечное затмение (относительные размеры тел и расстояния между ними условны)
Лунное затмение наступает, когда Луна, находясь на одной прямой с Солнцем и Землей, попадает в конусообразную тень, отбрасываемую Землей. Диаметр пятна тени Земли равен минимальному расстоянию Луны от Земли — 363 000 км, что составляет около 2,5 диаметра Луны, поэтому Луна может быть затенена целиком (см. рис. 3).
Лунные ритмы — это повторяющиеся изменения интенсивности и характера биологических процессов. Существуют лунно-месячные (29,4 сут) и лунно-суточные (24,8 ч) ритмы. Многие животные, растения размножаются в определенную фазу лунного цикла. Лунные ритмы свойственны многим морским животным и растениям прибрежной зоны. Так, у людей замечено изменение самочувствия в зависимости от фаз лунного цикла.
Существуют лунно-месячные (29,4 сут) и лунно-суточные (24,8 ч) ритмы. Многие животные, растения размножаются в определенную фазу лунного цикла. Лунные ритмы свойственны многим морским животным и растениям прибрежной зоны. Так, у людей замечено изменение самочувствия в зависимости от фаз лунного цикла.
Самый неизученный объект Солнечной системы
Введение.
Луна – особый объект Солнечной системы. Имеет свои НЛО, Земля живёт по лунному календарю. Главный объект поклонения у мусульман.
На Луне никто никогда не был (прибытие американцев на Луну – это мультфильм, снятый на Земле).
1. Глоссарий
| Свет | электромагнитная волна, воспринимаемая глазом | (4 – 7.5)*10 14 Гц(лямбда = 400-700 нм) | ||
| Световой год | Расстояние, проходимое светом за год | 0.3068 парсек = 9.4605*10 15 м | ||
| Парсек (пс) | Расстояние, с которого средний радиус земной орбиты (1 а. е), перпендикулярный углу зрения, виден под углом 1 секунда е), перпендикулярный углу зрения, виден под углом 1 секунда | 206265 а.е = 31*10 15 м | ||
| Диаметр нашейГалактики | 25000 парсек | |||
| Радиус Вселенной | 4*10 26 м | |||
| Сидерический месяц (S) | Это звёздный месяц – период движения Луны на небе относительно звёзд (полный оборот вокруг Земли) | 27.32166 = 27 суток 7 час 43 мин | ||
| Сидерический год (Т) | Период обращения земли вокруг Солнца | |||
| Синодический месяц (Р)Саросский цикл, или МЕТОН | ST = PT – PS смена фаз | 29.53059413580..29 д 12 ч 51 м 36″ | ||
| Драконический месяц (D) | Период обращения Луны относительно узлов её орбиты, т.е точек пересечения ею плоскости эклиптики | 27.21222 = 27 суток 5 час 5 мин | ||
| Аномалистический месяц (А) | Период обращения Луны относи-тельно перигея, ближайшей к земле точке её орбиты | 27. 55455 = 27 суток 13 час 18 мин 55455 = 27 суток 13 час 18 мин | ||
| Линия узлов Лунной орбиты медленно поворачивается навстречу движению Луны, совершая полный оборот за 18.6 года, тогда как большая ось Лунной орбиты поворачивается в ту же сторону, куда движется Луна, с периодом 8.85 года | ||||
| АПЕКС (направление движения Солнца) | Лямбда- Геркулес, расположено выше главной плоскости звёздной системы (смещение 6 пк) | |||
| Внешняя граница Солнечной системы (сфера Хилла) | 1 пк = 2*10 5 а.е. | |||
| Граница Солнечной системы (орбита Плутона) | ||||
| Астономическая единица – расстояние Земли до Солнца (а.е.) | ||||
| Расстояние С.С. от центральной плоскости Галактики | ||||
| Линейная скорость движения С.С. вокруг Галактического центра | ||||
СОЛНЦЕ
| Радиус | 6,96*10 5 км | |
| Периметр | 43,73096973*10 5 км | |
| Диаметр | 13,92*10 5 км | |
| Ускорение свободного падения на уровне видимой поверхности | 270 м/сек 2 | |
| Средний период вращения (Земных суток) | 25,38 | |
| Наклон экватора к эклиптике | 7,25 0 | |
| Дальность Солнечного ветра | 100 а. е. е. |
Прибыло 3 Луны. 2 Луны уничтожены планетой (Фаэтон), которая взорвала себя. Параметры оставшейся Луны:
Энциклопедия | ||
| Орбита – эллиптическая | ||
| Эксцентриситет | ||
| Радиус R | ||
| Диаметр | ||
| Окружность (периметр) | 10920,0692497 км | |
| Апогелий | ||
| Перигелий | ||
| Среднее расстояние | ||
| Барицентр системы Земля – Луна от центра масс Земли | ||
| Расстояние между центрами Земли и Луны: Апогелий — Перигей — | 379564.3 км, угол 38 ‘ 384640 км, угол 36 ‘ | |
| Наклон плоскости орбиты (к плоскости эклиптики) | 5 0 08 ‘ 43. | |
| Средняя скорость по орбите | 1.023 км/сек (3683 км/час) | |
| Суточная скорость видимого движения Луны среди звёзд | ||
| Период орбитального движения (сидерический месяц) = Периоду осевого вращения | 27.32166 сут. | |
| Смена фаз (Синодический месяц) | 29.5305941358 сут. | |
| Экватор Луны имеет постоянный наклон к плоскости эклиптики | 1 0 32 ‘ 47 “ | |
| Либрация по долготе | ||
| Либрация по широте | ||
| Наблюдаемая поверхность Луны | ||
| Угловой радиус (с Земли) видимого диска Луны (на среднем расстоянии) | 31 ‘ 05.16 “ | |
| Площадь поверхности | 3.796* 10 7 км 2 | |
| Объем | 2. | |
| Масса | 7.35*10 19 т (1/81.30 от м. З.) | |
| Средняя плотность | ||
| С Луны угол Земли | ||
| Плотность ионной структуры равномерна и составляет |
2. В состав ионной структуры входят ионные образования практически всей таблицы ионных структур кубической структуры с преобладанием S (серы) и радиоактивных редкоземельных элементов. Поверхность Луны сформирована путём напыления с последующим разогревом.
На поверхности Луны ничего нет.
Луна имеет две поверхности – внешнюю и внутреннюю.
Площадь внешней поверхности- 120*10 6 км 2 (код Луны – комплекс N 120), внутренней поверхности- 116*10 10 м 2 (маска кода).
Сторона, обращенная к Земле, тоньше на 184 км.
Центр тяжести располагается за геометрическим центром.
Все комплексы надежно защищены и не обнаруживают себя даже при работе.
В момент импульса (излучения) может не значительно измениться скорость вращения или орбита Луны. Компенсация – за счет направленного излучения октавы 43. Эта октава совпадает с октавой решетки Земли и не наносит вреда.
Комплексы на Луне предназначены в первую очередь, для поддержания автономного жизнеобеспечения, и во – вторых, для обеспечения (в случае избытка зарядового эквивалента) систем жизнеобеспечения на Земле.
Главная задача – не изменять альбедо Солнечной Системы, и за счет разностных характеристик, с учетом коррекции орбиты, эта задача выполнена.
Геометрически в существующий до этого закон формы, позволяющий выдерживать 28.5-дневный такт смены последовательности излучений (так называемые фазы Луны), идеально вписаны пирамиды коррекции, что завершило конструкцию комплексов.
Всего существует 4 фазы. Полная Луна имеет мощность излучения 1, остальные фазы – 3/4, 1/2, 1/4. Каждая фаза – 6.25 дней, 4 дня нет излучений.
Тактовая частота всех октав (кроме 54) – 128.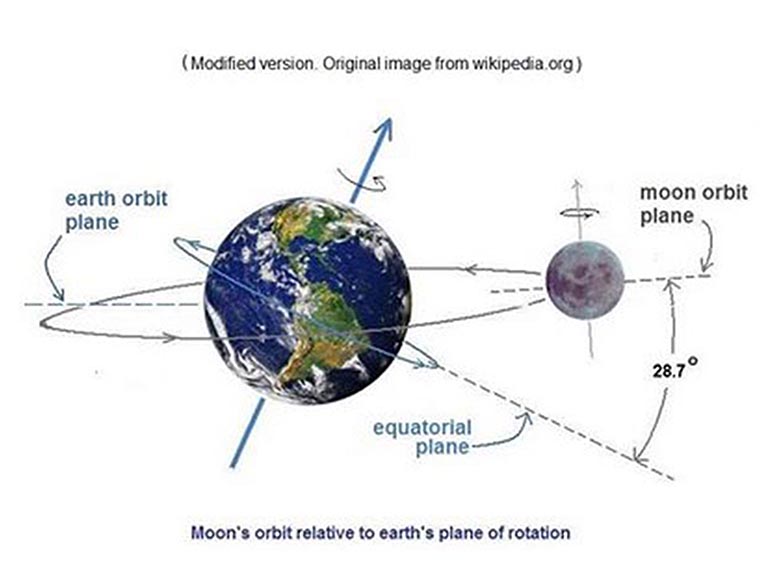 0, но плотность тактовой частоты мала, и поэтому яркость в оптическом диапазоне незначительна.
0, но плотность тактовой частоты мала, и поэтому яркость в оптическом диапазоне незначительна.
При коррекции орбиты используется тактовая частота 53.375. Но эта частота может изменить решетку верхнего слоя атмосферы, и может наблюдаться эффект дифракции.
В частности, с Земли количество Лун может быть 3, 6, 12, 24, 36. Этот эффект может продолжаться максимум 4 часа, после чего решетка восстанавливается за счет Земли.
Длительная коррекция (при нарушении альбедо Солнечной Системы) может привести к оптическому обману, но при этом возможна ликвидация слоя защиты.
3. Метрика пространства
Введение.
Известно, что атомные часы, установленные на вершине небоскреба и в его подвале, показывают разное время. Любое пространство связано с временем, и при установлении дальности и траектории необходимо представить не только конечный пункт следования, но и особенности преодоления этого пути в условиях изменения фундаментальных констант. Все аспекты, связанные с временем, будут приведены в “метрике времени”.
Целью настоящей главы является определение действительных значений некоторых фундаментальных констант, например, парсек. Кроме того, учитывая, особую роль Луны в системе жизнеобеспечения Земли, уточним некоторые понятия, остающиеся за рамками научных исследований, например, либрацию Луны, когда с Земли видно не 50 % поверхности Луны, а 59 %. Отметим также пространственную ориентацию Земли.
4. Роль Луны.
Науке известна огромная роль Луны в системе жизнеобеспечения Земли. Приведем лишь некоторые примеры.
— При полной Луне частичное ослабление силы притяжения Земли приводит к тому, что растения впитывают больше воды и микроэлементов из почвы, поэтому собранные в это время лечебные травы оказывают особенно сильное воздействие.
Луна, из-за близости к Земле, сильно воздействует своим гравитационным полем на Земную биосферу и вызывает, в частности, изменения магнитного поля Земли. Ритм Луны, приливов и отливов вызывает в биосфере изменения ночной освещенности, давления воздуха, температуры, действий ветра и магнитного поля Земли, а также уровня воды.
Рост растений и урожай зависят от звездного ритма Луны (период 27.3 дня), а активность животных, охотящихся ночью или вечером – от степени яркости Луны.
— При убывании Луны снижался рост растений, когда Луна прибывала – увеличивался.
— Полнолуние сказывается на росте преступности (агрессивности) у людей.
Время созревания яйцеклетки у женщин связано с ритмом Луны. Женщина склонна производить яйцеклетку в той фазе Луны, когда она родилась сама .
— При полнолунии и новолунии число женщин с менструацией достигает 100%.
— Во время убывающей фазы возрастает число рождаемых мальчиков, и понижается количество девочек.
— Свадьбы обычно проводят во время возрастания Луны.
— При возрастании Луны сеяли то, что растет над поверхностью Земли, при убывании – наоборот (клубни, коренья).
— Дровосеки рубят деревья при убывающей Луне , т.к. дерево содержит в это время меньше влаги и дольше не подвергается гниению.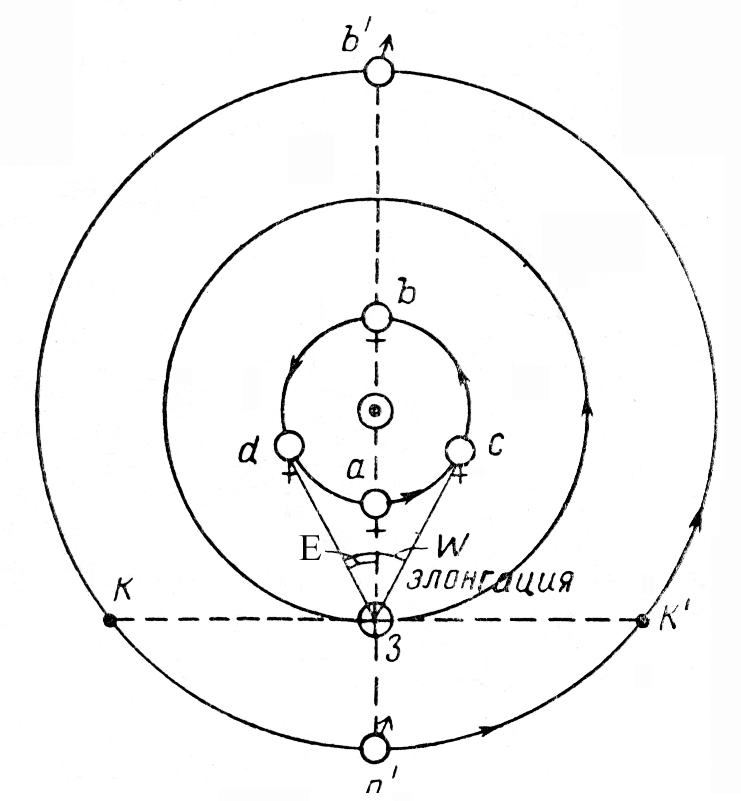
При полнолунии и новолунии наблюдается тенденция к уменьшению мочевой кислоты в крови, 4 – й день после новолуния – самые низкие показатели.
— Прививки при полнолунии обречены на провал.
— При полнолунии ухудшаются легочные заболевания, коклюш, аллергия.
— Цветное зрение у человека подчиняется лунной периодичности .
— При полнолунии – повышенная активность, при новолунии – пониженная.
— Подстригаться принято при полнолунии.
— Пасха – первое воскресенье после весеннего равноденствия, первый день
Полнолуния.
Таких примеров можно привести сотни, но уже то, что Луна существенно влияет на все аспекты жизни на Земле, видно из вышеприведенных примеров. Что мы знаем о Луне? Это то, что приведено в таблицах по Солнечной системе.
Известно также, что Луна не “лежит” в плоскости орбиты Земли:
Действительное назначение Луны, особенностей ее структуры, назначения приведены в приложении, и тогда то и возникают вопросы по времени и пространству – насколько согласовано все с действительным состоянием Земли как неотъемлемой частью Солнечной Системы.
Рассмотрим состояние главной астрономической единицы – парсек на основании тех данных, которыми располагает современная наука.
5. Астрономическая единица измерений .
За 1 год Земля, двигаясь по орбите Кеплера, возвращается в исходную точку. Известен эксцентриситет орбиты Земли – апогелий и перигелий. На основании точного значения скорости движения Земли (29.765 км/сек) определено расстояние до Солнца.
29.765 * 365.25 * 24 * 3600 = 939311964 км – это длина пути за год.
Отсюда, радиус орбиты (без учета эксцентриситета) = 149496268,4501 км, или 149.5 млн. км. Это значение и взято за базовую астрономическую единицу – парсек .
В этой единице измерен весь Космос.
6. Действительное значение астрономической единицы расстояния.
Если оставить то, что за астрономическую единицу расстояния необходимо взять расстояние от Земли до Солнца, то ее значение несколько другое. Известны 2 значения: абсолютная скорость движения Земли V = 29. 765 км/сек и угол наклона экватора Земли к эклиптике = 23 0 26 ‘ 38 “ , или 23.44389 0 . Если подвергнуть сомнению эти два значения, вычисленные с абсолютной точностью за время многовековых наблюдений, значит разрушить все, что известно о Космосе.
765 км/сек и угол наклона экватора Земли к эклиптике = 23 0 26 ‘ 38 “ , или 23.44389 0 . Если подвергнуть сомнению эти два значения, вычисленные с абсолютной точностью за время многовековых наблюдений, значит разрушить все, что известно о Космосе.
Теперь настала пора приоткрыть некоторые тайны, которые и так были известны, но на них никто не обращал внимания. Это во-первых то, что Земля двигается в пространстве по спирали, а не по орбите Кеплера . Известно, что Солнце перемещается, но оно перемещается вместе со всей Системой, значит движение Земли происходит по спирали. Второе – это то, что сама Солнечная Система находится в поле действия Гравитационного репера . Что это такое, будет показано ниже.
Известно наличие смещения центра гравитационной массы Земли в сторону Южного полюса на 221.6 км. Однако Земля двигается в обратном направлении. Если бы Земля просто двигалась бы по орбите Кеплера, по всем законам движения гравитационной массы движение было бы вперед Южным полюсом, а не Северным.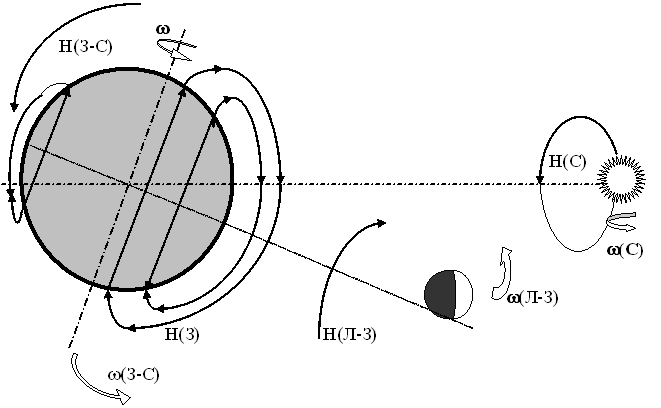
Волчка здесь не получается из-за того, что инерционная масса приняла бы нормальное положение – Южным полюсом в сторону движения.
Однако любой волчок может совершать вращение со смещенной гравитационной массой только в одном случае – когда ось вращения строго перпендикулярна плоскости.
Но на волчок действуют не только сопротивление среды (вакуума), давление всех излучений от Солнца, взаимное гравитационное давление других структур Солнечной Системы. Поэтому угол, равный 23 0 26 ‘ 38 ” именно с учетом всех внешних воздействий, включая воздействия гравитационного репера. Орбита Луны имеет обратный угол к орбите Земли и это, как будет показано ниже, не соотносится с расчетными константами. Представим себе цилиндр, на который ” намотана” спираль. Шаг спирали = 23 0 26 ‘ 38 “ . Радиус спирали равен радиусу цилиндра. Развернем один виток этой спирали на плоскость:
Расстояние от точки О до точки А (апогей и апогей) равно 939311964 км.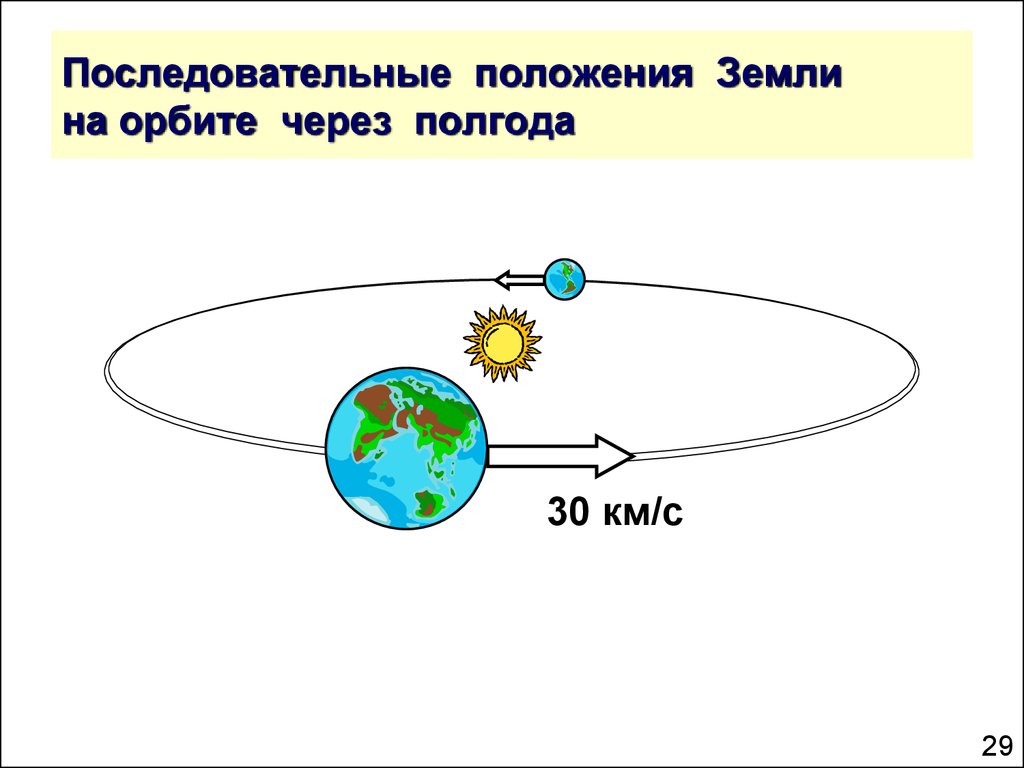
Тогда длина орбиты Кеплера: ОВ = ОА*cos 23.44839 = 861771884,6384 км , отсюда расстояние от центра Земли до центра Солнца будет равно 137155371,108 км, то есть несколько меньше того значения, которое известно (на 12344629 км) – почти на 9 %. Много это или мало, посмотрим на простом примере. Пусть скорость света в вакууме составляет 300000 км/сек. При значении 1 парсек = 149.5 млн. км время прохождения Солнечного луча от Солнца до Земли составляет 498 сек, при значении 1 парсек = 137.155 млн. км это время будет составлять 457 сек, то есть на 41 секунду меньше.
Эта разность почти в 1 минуту имеет колоссальное значение, так как во-первых, меняются все расстояния в Космосе, и во-вторых, нарушается тактовый интервал систем жизнеобеспечения, причем накопленная или не добранная мощность систем жизнеобеспечения может привести к срыву работы самой системы.
7. Гравитационный репер.
Известно, что плоскость эклиптики имеет наклон относительно силовых линий гравитационного репера, но направление движения – перпендикулярно этим силовым линиям.
8. Либрация Луны. Рассмотрим уточненную схему орбиты Луны:
Учитывая то, что Земля двигается по спирали, а также прямое воздействие гравитационного репера, на Луну этот репер также оказывает прямое воздействие, что видно из схемы расчета углов.
9. Практическое использование константы “парсек”.
Как было показано ранее, значение константы “парсек” существенно отличается от той величины, которая используется в повседневной практике. Рассмотрим несколько примеров использования этой величины.
9.1. Контроль времени.
Как известно, любое событие на Земле происходит во времени. Кроме того, известно, что любой космический объект, обладающий неинерционной массой, имеет собственное время, которое обеспечено тактовым генератором высокой октавы. Для Земли это 128 октава, и такт = 1 секунде (биологический такт немного отличается – коллайдеры Земли дают такт 1.0007 секунды). Инерционная масса имеет время жизни, определяемое плотностью зарядового эквивалента и его значением при связи ионных структур. Любая неинерционная масса обладает магнитным полем, и скорость распада магнитного поля определяется временем распада верхней структуры и потребностью более низких (ионных) структур в этом распаде. Для Земли, учитывая ее Вселенский масштаб, принято единое время, которое измеряется в секундах, и время – функция пространства, которое проходит Земля за один полный оборот, поступательно двигаясь по спирали вслед за Солнцем.
Любая неинерционная масса обладает магнитным полем, и скорость распада магнитного поля определяется временем распада верхней структуры и потребностью более низких (ионных) структур в этом распаде. Для Земли, учитывая ее Вселенский масштаб, принято единое время, которое измеряется в секундах, и время – функция пространства, которое проходит Земля за один полный оборот, поступательно двигаясь по спирали вслед за Солнцем.
В таком случае должна быть некоторая структура, которая производит отсечку “0” времени и относительно этого времени производить определенные манипуляции с системами жизнеобеспечения. Не имея такой структуры, невозможно обеспечить как устойчивое положение самой системы жизнеобеспечения, так и связи системы.
Ранее рассматривалось движение Земли, и было выведено, что радиус орбиты Земли существенно (на 12344629 км) отличается от принятого во всех известных расчетах.
Если принять скорость распространения гравито-магнито-электроволны в Космосе V = 300000 км/сек, то эта разность орбит даст 41.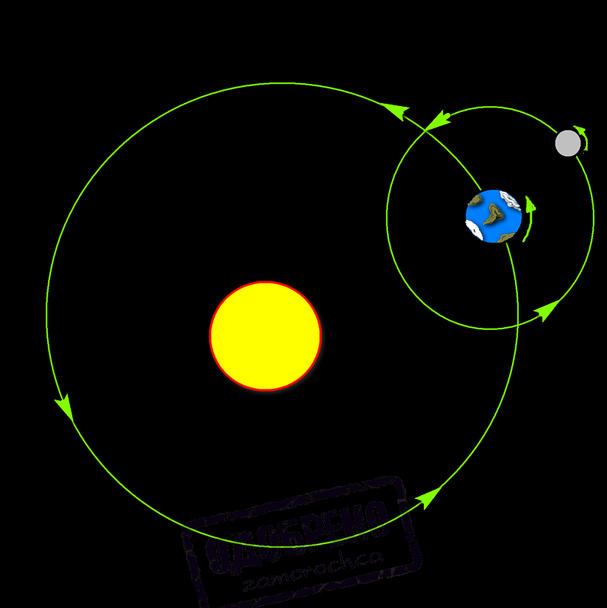 15 сек.
15 сек.
Можно не сомневаться, что только это значение внесет существенные коррективы не только в проблемы решения задач жизнеобеспечения, но крайне важно – в связь, то есть сообщения попросту могут не доходить до назначения, чем могут воспользоваться иные цивилизации.
Отсюда – надо понимать, какую огромную роль играет функция времени даже в неинерционных системах, поэтому рассмотрим еще раз то, что всем хорошо известно.
9.2. Автономные структуры контроля систем координации.
Необычно – но к системе именно координации следует отнести пирамиду Хеопса в Эль-Гизе (Египет) – 31 0 восточной долготы и 30 0 северной широты.
Общий путь Земли за один оборот составляет 939311964 км, тогда проекция на орбиту Кеплера: 939311964 * cos (25.25) 0 = 849565539,0266.
Радиус R исх = 135212669,2259 км. Разность между исходным и текущим состоянием составляет 14287330,77412 км, то есть проекция орбиты Земли изменилась на t = 47,62443591374 сек.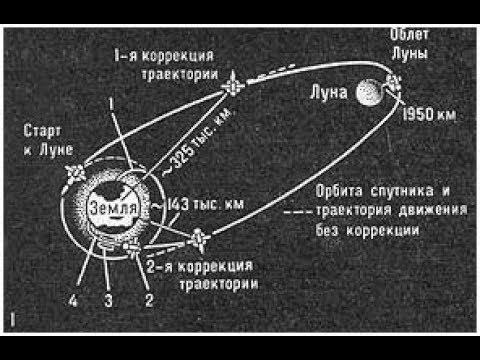 Много это или мало- зависит от назначения систем управления и длительностью связи.
Много это или мало- зависит от назначения систем управления и длительностью связи.
10. Исходный репер.
Местоположение исходного репера – 37 0 30 ‘ восточной долготы и 54 0 22 ‘ 30 “ северной широты. Наклон оси репера составляет 3 0 37 ‘ 30 “ к Северному полюсу. Направление репера: 90 0 – 54 0 22 ‘ 30 “ – 3 0 37 ‘ 30 = 32 0 .
Используя Звездную карту, находим, что исходный репер направлен на созвездие Большой медведицы, звезда Мегрец (4 – я звезда). Следовательно, исходный репер был создан уже при наличии Луны. Заметим, что именно эта звезда больше всех интересует астрономов (см. Н.Морозова “Христос”). Кроме того, эта звезда названа именем Ю.Лужкова (других звёзд не было).
11. Ориентация.
Третье замечание – Лунные циклы. Как известно, не Юлианский календарь (Метон) имеет 13 месяцев, но если привести полную таблицу оптимальных дней (Пасха), то увидим серьезное смещение, которое не было учтено при расчетах. Это смещение, выраженное в секундах, уводит нужную дату далеко от оптимальной точки.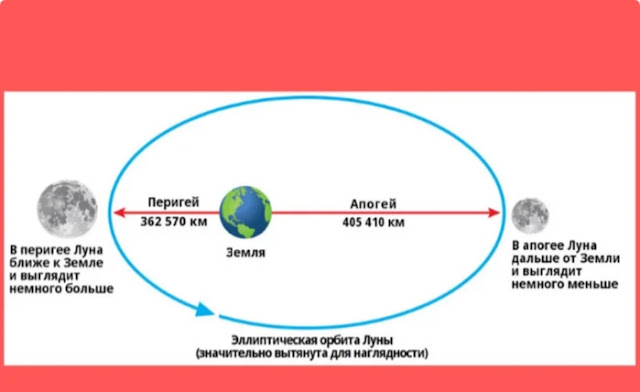
| Рассмотрим следующую схему:После появления Луны за счет изменения угла наклона экватора на 1 0 48 ‘ 22 “ произошло смещение орбиты Земли. При сохранении положения начального репера, который на сегодня уже ничего не определяет, остался только исходный репер, но то, что будет показано ниже, может на первый взгляд показаться маленьким недоразумением, легко поправимым. Однако здесь и кроется то, что в состоянии привести любую систему жизнеобеспечения к развалу. Первое относится, как было указано ранее – к изменению времени движения Земли от апогея до апогея. Второе – Луна, как показали наблюдения, имеет тенденцию изменять поправочный член во времени, и это видно из таблицы: Ранее указывалось, что орбита Луны по отношению к орбите Земли имеет наклон: | ||
Углы группы А:
5 0 18 ‘ 58.42 “ – апоглией,
5 0 17 ‘ 24.84 “ – перигелий
Углы группы В:
4 0 56 ‘ 58.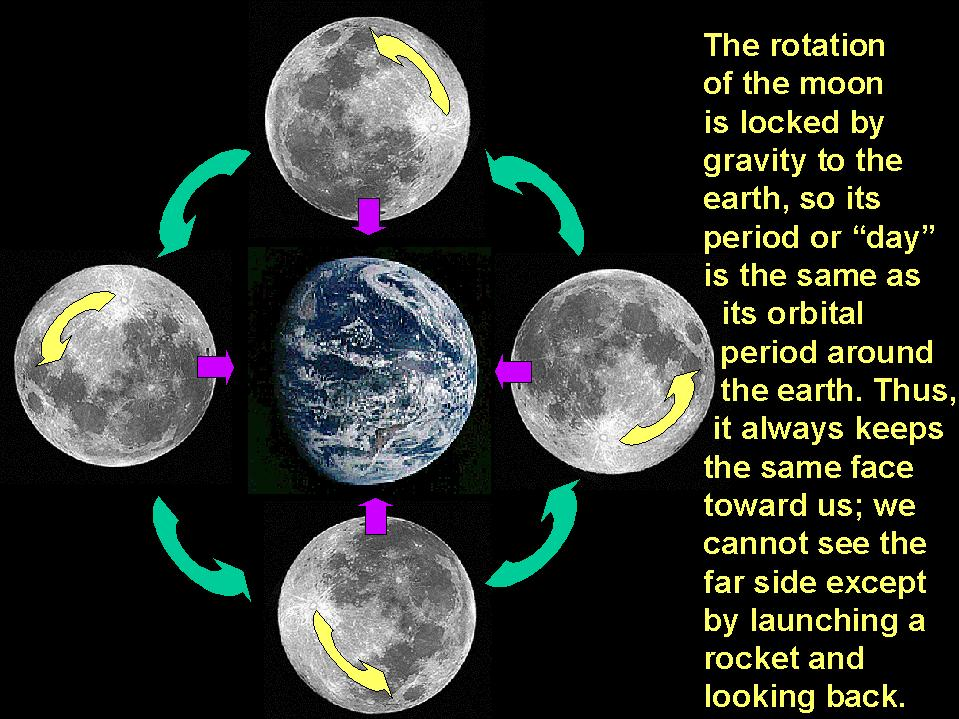 44 “ – апогелий,
44 “ – апогелий,
4 0 58 ‘ 01 “ – перигелий
Однако вводя поправочный член, получим иные значения для орбиты Луны.
12. С В Я З Ь
Энергетические характеристики:
Передача: ЭИ = 1.28*10 -2 вольт*м 2 ; МИ = 4.84*10 -8 вольт/м 3 ;
Эти два ряда определяют только алфавитную группу и знак системы символа, и не всегда используются все углы.
При использовании всех углов мощность повышается в 16 раз.
Для кодирования используется 8 – разрядная азбука:
DO RE MI FA SOL LA SI NA.
Главные тона знака не имеют, т.е. 54 октава определяет главный тон. Разделитель – 62 октава потенциала. Между двумя смежными углами – дополнительная разбивка на 8, поэтому один угол содержит весь алфавит. Положительный ряд предназначен для кодирования команд, приказов и распоряжений (таблица кодирования), отрицательный ряд содержит текстовуюинформацию (таблица – словарь).
При этом используется 22 – знаковая азбука, известная на Земле . Используется подряд 3 угла, последние знаки последнего угла – это точка и запятая. Чем значимее текст, тем более высокие октавы углов используются.
Используется подряд 3 угла, последние знаки последнего угла – это точка и запятая. Чем значимее текст, тем более высокие октавы углов используются.
Текст сообщения:
1. Кодовый сигнал – 64 знака + 64 пропуска (fa). 6 раз повторить
2. Текст сообщения – 64 знака + 64 пропуска и 6 раз повторить, если текст срочный, то 384 знака, остальное – пропуски (384) и нет повторений.
3. Ключ текста – 64 знака + 64 пропуска (повторяются 6 раз).
Учитывая наличие пропусков, на принимаемый или передаваемый тексты накладывается математический шнур ряда Фибоначчи, и поступление текста – непрерывное.
Второй математический шнур отсекает красное смещение.
По второму кодовому сигналу устанавливается тип отсечки и прием (передача) ведутся в автоматическом режиме.
Общая длина сообщения составляет 2304 знака,
время приема- передачи- 38 минут 24 сек.
Замечание. Главный тон – это не всегда 1 знак. При повторении знака (режим срочного исполнения) используется дополнительный ряд:
Таблица командной строки Таблица повторения команды
53. | |||||||||||||||||
53.12501250 | |||||||||||||||||
53.25002500 | |||||||||||||||||
53.37503750 | |||||||||||||||||
53.50005000 | |||||||||||||||||
53. | |||||||||||||||||
53.75007500 | |||||||||||||||||
53.87508750 |
Дешифровка сообщений производилась в автоматическом режиме с использованием таблицы перекодировки в соответствии с частотными параметрами позвоночника, если команды предназначались людям. Это – полная 2-я октава пианино, 12 символов, таблица 12*12, в которой до 1266 года размещался Иврит, до 2006 года – английский язык, и с Пасхи 2007 года – русский алфавит (33 буквы).
В таблице размещены цифры (12-я система счисления), знаки типа “+”, “$” и прочие, а также служебные символы, включая маски кодов.
13. Внутри Луны располагается 4 комплекса:
Комплекс | Пирамиды | Октавы А | Октавы | Октавы С | Октавы Д | ||
Изменяемая геометрия (все наборы частот) | |||||||
Фиксированная геометрия | |||||||
Фиксированная геометрия | |||||||
Фиксированная геометрия | |||||||
Октавы А – вырабатывают сами пирамиды
Октавы В – получают с Земли (Солнца – *)
Октавы С – находятся в трубке связи с Землёй
Октавы Д – находятся в трубке связи с Солнцем
14. Светимость Луны.
Светимость Луны.
При сбросе Программ на Землю наблюдается гало – кольца вокруг Луны (всегда в фазе III).
15. Архив Луны.
Однако её возможности ограничены – комплекс состоял из 3 Лун, 2 были уничтожены (метеоритный пояс – это бывшая планета, в которой Система Управления взорвала себя вместе со всеми объектами (НЛО), которые добрались до секретов существования системы планет.
В определённое время остатки планеты в виде метеоритов осыпаются и на Землю, и в основном – на Солнце, создавая на нём черные пятна.
16. Пасха.
Все Системы Управления Земли синхронизированы по такту, задаваемым Солнцем, с учётом движения Луны. Движение Луны вокруг Земли – это Синодический месяц (Р)Саросский цикл, или МЕТОН. Расчёт – по формуле ST = PT -PS. Вычисленное значение = 29.53059413580.. или 29 д 12 ч 51 м 36″.
Население Земли разделено на 3 генотипа: 42 (основное население, более 5 млрд чел.), 44 (“золотой миллиард”, имеющие мозг, привезённый со спутников планет) и 46 (“золотой миллион”, 1200000 человек, сброшенных с планеты Солнце).
Заметим, что Солнце – это планета, а не Звезда, её размер не превышает размер Земли. Для перевода генотипа 42 в 44 и 46 существует Пасха, или определённый день, когда Луна производит сброс Программ. До 2009 года все Пасхи проводились только в III фазе Луны.
К 2009 году формирование генотипов 44 и 46 завершено и можно уничтожить генотип 42, потому Пасха 2009-04-19 будет проходить в новолуние (фаза I), и Системы Управления Земли будут уничтожать генотип 42 в условиях изъятия Луной остатков мозга. На уничтожение отводится 3 года (2012 год – завершение). Раньше существовал недельный цикл, начинающийся 9 Аб, при котором все, у кого изъяли старый мозг, а новый не подошёл, уничтожались (холохост). Структура календаря:
По Метону работают Системы Управления, но на Земле (в церквах, костёлах, синагогах) используют юлианский или григорианский календарь, которые учитывают только движение Земли (среднее значение за 4 года 365.25 дня).
Полный цикл (19 лет) Метона и 19 лет григорианского календаря примерно совпадают (с точностью до часов). Потому, зная Метон и совмещая его с григорианским календарём, можно радостно встречать своё преобразование.
Потому, зная Метон и совмещая его с григорианским календарём, можно радостно встречать своё преобразование.
17. Объекты Луны (НЛО).
Все “лунатики” находятся внутри Луны. Атмосфера Луны необходима только для контроля и существование в этой атмосфере без средств защиты невозможно.
Для контроля за поверхностью и атмосферой Луна располагает собственными объектами (НЛО). Это – в основном автоматы, но часть из них пилотируемые.
Максимальная высота подъёма не превышает 2 км от поверхности. “Лунатики” не предназначены для жизни на Земле, они имеют достаточно комфортные условия для ведения работы и отдыха. Всего на Луне 242 объекта (36 типов), из них 16 пилотируемые. Аналогичные объекты имеются на некоторых спутниках (и на Фобосе тоже).
18. Защита Луны.
Луна – единственный спутник, имеющий связь с Суром – планетой под Мегрец, 4 звезда Большой Медведицы.
19. Система дальней связи.
Система связи – на 84 октаве, но эту октаву формирует Земля. Связь с Суром требует огромных энергетических затрат (октава 53.5). Связь возможна только после весеннего равноденствия, в течение 3 месяцев. Скорость света – это относительная величина (относительно 128 октавы) и потому относительно 84 октавы скорость в 2 20 ниже. За один сеанс можно передать 216 символов (включая служебные). Связь – только после завершения цикла по Метону. Число сеансов – 1. Следующий сеанс примерно через 11.4 года, при этом энергообеспечение Солнечной системы падает на 30%.
Связь с Суром требует огромных энергетических затрат (октава 53.5). Связь возможна только после весеннего равноденствия, в течение 3 месяцев. Скорость света – это относительная величина (относительно 128 октавы) и потому относительно 84 октавы скорость в 2 20 ниже. За один сеанс можно передать 216 символов (включая служебные). Связь – только после завершения цикла по Метону. Число сеансов – 1. Следующий сеанс примерно через 11.4 года, при этом энергообеспечение Солнечной системы падает на 30%.
20. Вернёмся к фазам Луны.
Номер 1 = новолуние,
2 = молодой месяц (при этом диаметр Земли примерно равен диаметру Луны),
3 = первая четверть (диаметр Земли больше действительного диаметра Земли),
4 = Луну распилили пополам. В физической энциклопедии утверждается, что это угол 90 0 (Солнце – Луна – Земля). Но этот угол может существовать 3 – 4 часа, но мы видим это состояние в течение 3 дней.
Номер 5 – какая форма Земли даёт такое “отражение”?
Заметим, что Луна вращается вокруг Земли и если верить энциклопедии, то смену всех 10 фаз мы должны наблюдать в течение одних суток.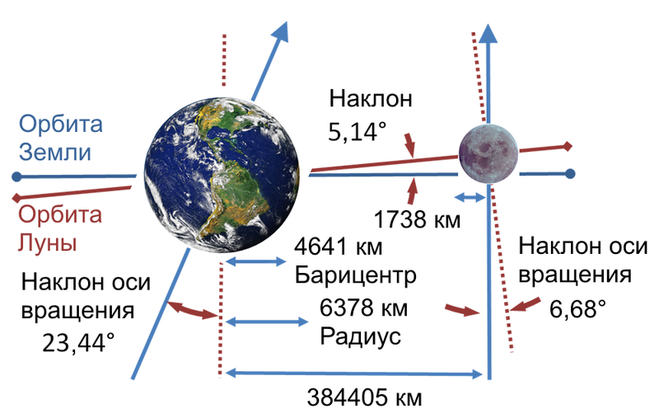
Луна ничего не отражает, и если Комплексы Луны в связи с ликвидацией ряда частот в трубке связи Луна – Земля отключатся, то Луну мы больше не увидим. Кроме того, ликвидация некоторых гравитационных частот в трубке связи Луна – Земля отодвинет Луну в условиях не работающих Лунных Комплексов на расстояние не менее 1 млн. км.
Луна сопровождает нашу планету в её большом космическом путешествии вот уже несколько миллиардов лет. И показывает она нам, землянам, из века в век всегда один и тот же свой лунный пейзаж. Почему мы любуемся только одной стороной нашего спутника? Вращается ли Луна вокруг своей оси или же парит в космическом пространстве неподвижно?
Характеристики нашего космического соседа
В Солнечной системе имеются спутники гораздо крупнее Луны. Ганимед — спутник Юпитера, к примеру, в два раза тяжелее Луны. Но зато она — самый большой спутник относительно материнской планеты. Её масса составляет более процента от земной, а диаметр — около четверти земного.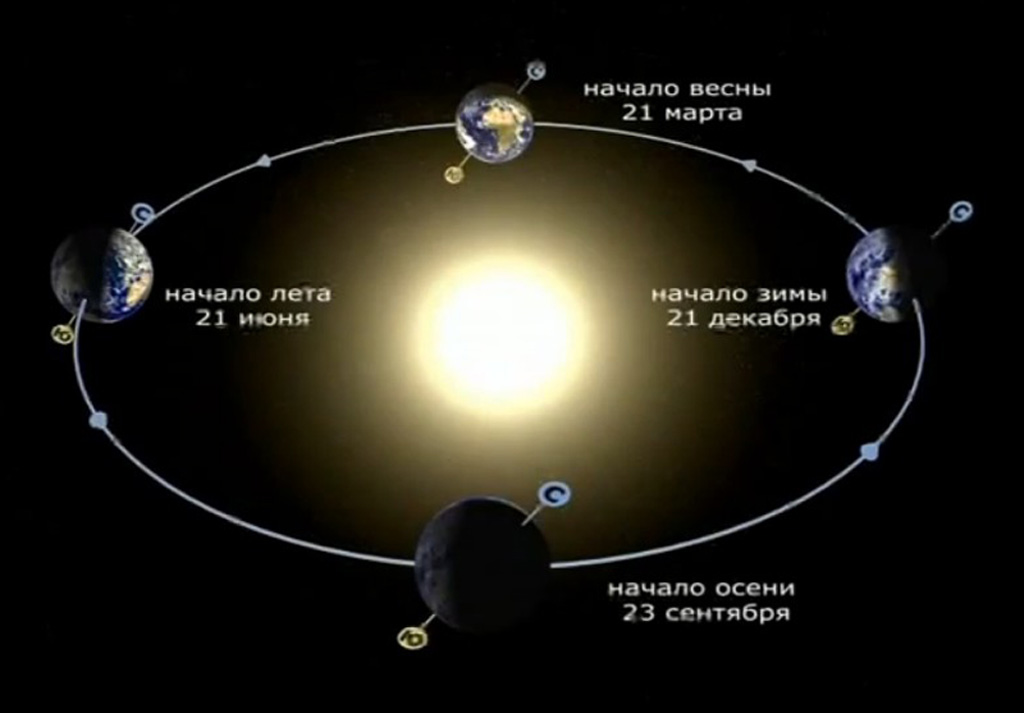 Таких пропорций в солнечной семье планет больше нет.
Таких пропорций в солнечной семье планет больше нет.
Давайте попытаемся ответить на вопрос о том, вращается ли Луна вокруг своей оси, присмотревшись повнимательнее к ближайшему нашему космическому соседу. По принятой сегодня в научных кругах теории, естественный спутник наша планета приобрела будучи ещё протопланетой — не до конца остывшей, покрытой океаном жидкой раскалённой лавы, в результате столкновения с другой планетой, меньшей по размеру. Поэтому химические составы лунного и земного грунтов слегка отличаются — тяжёлые ядра столкнувшихся планет слились, из-за чего земные породы богаче железом. Луне же достались остатки верхних слоёв обеих протопланет, там больше камня.
Вращается ли Луна
Если быть точным, то вопрос о том, вращается ли Луна, не совсем корректный. Ведь как и любой спутник в нашей системе, она оборачивается около материнской планеты и вместе с ней кружится вокруг светила. А вот, Луны не совсем обычно.
Сколько ни смотри на Луну, она всегда повёрнута к нам кратером Тихо и морем Спокойствия. «А вращается ли Луна вокруг своей оси?» − из века в век задавали себе вопрос земляне. Строго говоря, если оперировать геометрическими понятиями, ответ зависит от выбранной системы координат. Относительно Земли осевое вращение у Луны и вправду отсутствует.
«А вращается ли Луна вокруг своей оси?» − из века в век задавали себе вопрос земляне. Строго говоря, если оперировать геометрическими понятиями, ответ зависит от выбранной системы координат. Относительно Земли осевое вращение у Луны и вправду отсутствует.
А вот с точки зрения наблюдателя, расположенного на линии Солнце-Земля, осевое вращение Луны будет хорошо заметно, причём один полярный оборот до доли секунды окажется равен по длительности орбитальному.
Интересно, что явление это в Солнечной системе не уникально. Так, спутник Плутона Харон всегда смотрит на свою планету одним боком, точно так же ведут себя спутники Марса — Деймос и Фобос.
На научном языке это называется синхронным вращением или приливным захватом.
Что такое прилив?
Для того чтобы понять суть этого явления и уверенно ответить на вопрос о том, вращается ли Луна вокруг собственной оси, необходимо разобрать суть приливных явлений.
Представим себе две горы на поверхности Луны, одна из которых «смотрит» прямо на Землю, другая же находится в противоположной точке лунного шара. Очевидно, что если бы обе горы не были частью одного небесного тела, а вращались вокруг нашей планеты самостоятельно, их вращение не могло бы быть синхронным, та что ближе, по законам ньютоновской механики, должна вращаться быстрее. Именно поэтому массы лунного шара, расположенные в противоположных по направлению к Земле точках, стремятся «убежать друг от друга».
Очевидно, что если бы обе горы не были частью одного небесного тела, а вращались вокруг нашей планеты самостоятельно, их вращение не могло бы быть синхронным, та что ближе, по законам ньютоновской механики, должна вращаться быстрее. Именно поэтому массы лунного шара, расположенные в противоположных по направлению к Земле точках, стремятся «убежать друг от друга».
Как «остановилась» Луна
Как действуют приливные силы на то или иное небесное тело, удобно разобрать на примере нашей собственной планеты. Мы ведь тоже вращаемся вокруг Луны, а точнее Луна и Земля, как и положено в астрофизике, «водят хоровод» вокруг физического центра масс.
В результате действия приливных сил и в ближайшей, и в наиболее удалённой от спутника точке уровень воды, покрывающей Землю, поднимается. Причём максимальная амплитуда прилива-отлива может достигать 15 и более метров.
Ещё одной особенностью данного явления является то, что эти приливные «горбы» ежесуточно огибают поверхность планеты против её вращения, создавая трение в точках 1 и 2, и таким образом потихоньку останавливают Земной шар в его вращении.
Воздействие же Земли на Луну гораздо сильнее из-за разности масс. И хотя на Луне нет океана, на каменные породы приливные силы действуют ничуть не хуже. И результат их работы налицо.
Так вращается ли Луна вокруг своей оси? Ответ положительный. Но вращение это тесно связано с движением вокруг планеты. Приливные силы за миллионы лет выровняли осевое вращение Луны с орбитальным.
А что же Земля?
Астрофизики утверждают, что сразу после большого столкновения, ставшего причиной образования Луны, вращения нашей планеты была намного больше, чем сейчас. Сутки длились не более пяти часов. Но в результате трения приливных волн о дно океана год за годом, тысячелетие за тысячелетием вращение замедлялось, и нынешние сутки длятся уже 24 часа.
В среднем каждый век прибавляет нашим суткам по 20-40 секунд. Учёные предполагают, что через пару миллиардов лет наша планета будет смотреть на Луну так же, как и Луна на неё, то есть одной стороной. Правда этого, скорее всего, не произойдёт, так как ещё раньше Солнце, превратившись в красного гиганта, «проглотит» и Землю, и ее верного спутника — Луну.
Кстати, приливные силы дарят землянам не только повышение и понижение уровня мирового океана в районе экватора. Воздействуя на массы металлов в земном ядре, деформируя горячий центр нашей планеты, Луна помогает поддерживать его в жидком состоянии. А благодаря активному жидкому ядру, наша планета имеет собственное магнитное поле, защищающее всю биосферу от убийственного солнечного ветра и смертоносных космических лучей.
В очень древние времена люди не имели правильного представления о форме и размерах нашей планеты и о том, какое место она занимает в пространстве. Теперь мы знаем, что физическая поверхность Земли, представляющая сочетание суши и водных пространств, в геометрическом отношении имеет весьма сложную форму; ее нельзя представить ни одной из известных и математически изученных геометрических фигур. На поверхности Земли моря и океаны занимают около 71 %, а суша — около 29 %; самые же высокие горы и самые большие глубины океанов по сравнению с размерами всей Земли ничтожно малы. Так, например, на глобусе диаметром 60 см гора Эверест высотой приблизительно 8840 м изобразится всего лишь крупинкой в 0,25 мм. Поэтому за общую — теоретическую — форму Земли принимают тело, ограниченное поверхностью океанов, находящейся в спокойном состоянии, мысленно продолженной под всеми материками. Эта поверхность называется геоидом (гео — по-гречески «земля»). В первом же приближении фигуру Земли считают эллипсоидом вращения (сфероидом) — поверхностью, образованной в результате вращения эллипса вокруг своей оси.
Так, например, на глобусе диаметром 60 см гора Эверест высотой приблизительно 8840 м изобразится всего лишь крупинкой в 0,25 мм. Поэтому за общую — теоретическую — форму Земли принимают тело, ограниченное поверхностью океанов, находящейся в спокойном состоянии, мысленно продолженной под всеми материками. Эта поверхность называется геоидом (гео — по-гречески «земля»). В первом же приближении фигуру Земли считают эллипсоидом вращения (сфероидом) — поверхностью, образованной в результате вращения эллипса вокруг своей оси.
Размеры земного сфероида определялись неоднократно, но наиболее фундаментальные из них были установлены в 1940 г. в СССР Ф. Н. Красовским (1873–1948) и А. А. Изотовым (1907–1988): по их определениям малая ось земного сфероида, совпадающая с осью вращения Земли, b = 6356,86 км, а большая полуось, перпендикулярная малой оси и лежащая в плоскости земного экватора, a = 6378,24 км.
Отношение α = (a — b)/a , называемое сжатием земного сфероида, равно 1/298,3.
В 1964 г. решением Международного астрономического союза (MAC) для земного сфероида принято a = 6378,16 км, b = 6356,78 км и α = 1:298,25, что весьма близко к результатам, полученным советскими учеными в 1940 г. и принятыми постановлением Совета Министров СССР от 7 апреля 1946 г. за основные для всех астрономо-геодезических и картографических работ, выполняемых в нашей стране.
Находясь в любой точке земной поверхности, мы довольно скоро обнаруживаем, что все видимое на небосводе (Солнце, Луна, звезды, планеты) вращается вокруг нас как одно целое. На самом деле это явление кажущееся, оно является следствием вращения Земли вокруг своей оси с запада на восток, т. е. в направлении, противоположном кажущемуся суточному вращению небесного свода вокруг оси мира , представляющей прямую, параллельную оси вращения Земли, концами которой являются северный и южный полюсы нашей планеты. Вращение Земли вокруг своей оси можно доказать разными способами. Но теперь его можно непосредственно наблюдать с помощью космических аппаратов.
Но теперь его можно непосредственно наблюдать с помощью космических аппаратов.
В древние времена люди полагали, что Солнце, перемещаясь относительно звезд, обходит нашу планету по кругу в течение одного года, Земля же будто бы неподвижна и находится в центре Вселенной. Такого представления о мироздании придерживались и древние астрономы. Оно нашло отражение в знаменитом сочинении древнегреческого астронома Клавдия Птолемея (II в.), написанном в середине II в. и известном под искаженным названием «Альмагест» . Такая система мира получила название геоцентрической (от того же слова «гео»).
Новый этап в развитии астрономии начинается с опубликования в 1543 г. книги Николая Коперника (1473–1543) «О вращении небесных сфер», в которой изложена гелиоцентрическая (гелиос — «солнце») система мира, отражающая действительное строение Солнечной системы. Согласно теории Н. Коперника центром мира является Солнце, вокруг которого движутся шарообразная Земля и все подобные ей планеты и притом в одном направлении, вращаясь каждая относительно одного из своих диаметров, и что только Луна вращается вокруг Земли, являясь его постоянным спутником, и вместе с последней движется вокруг Солнца, при этом примерно в одной и той же плоскости.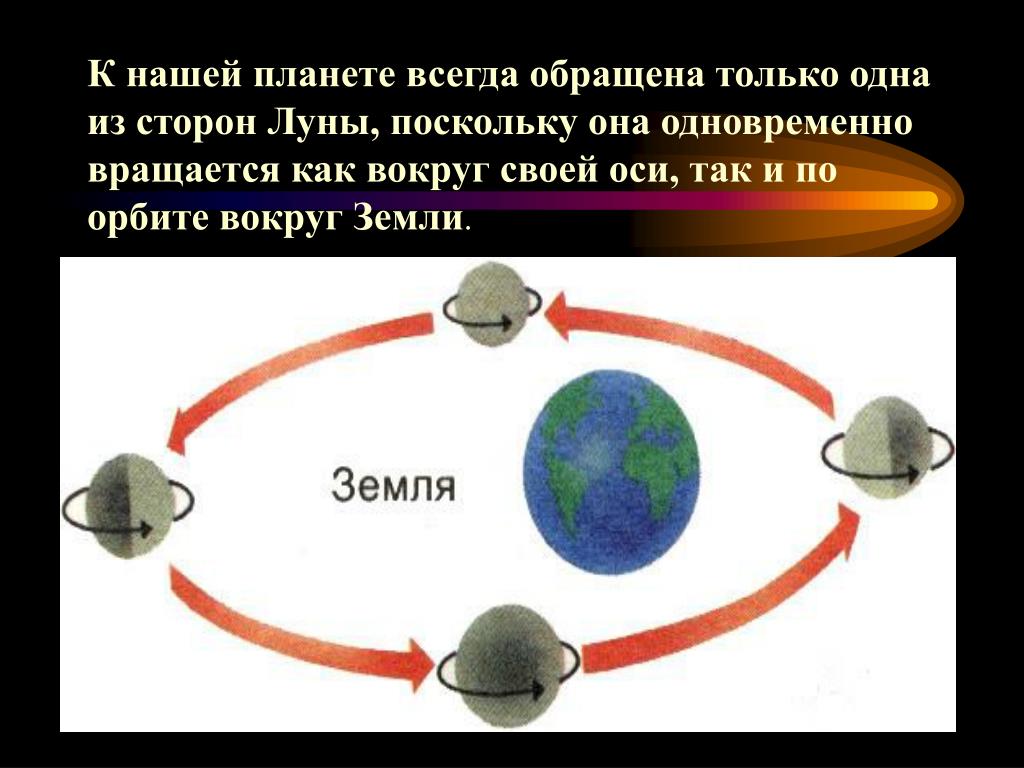
Рис. 1. Видимое движение Солнца
Для определения положения тех или иных светил на небесной сфере необходимо иметь «опорные» точки и линии. И здесь прежде всего используется отвесная линия, направление которой совпадает с направлением силы тяжести. Продолженная вверх и вниз эта линия пересекает небесную сферу в точках Z и Z» (рис. 1), называемых соответственно зенитом и надиром .
Большой круг небесной сферы, плоскость которого перпендикулярна линии ZZ», называется математическим или истинным горизонтом . Ось РР», вокруг которой вращается в своем видимом движении небесная сфера (это ее вращение является отражением вращения Земли), и называется осью мира: она пересекает поверхность небесной сферы в двух точках — северном Р и южном Р» полюсах мира .
Большой круг небесной сферы QLQ»F, плоскость которого перпендикулярна оси мира РР», является небесным экватором ; он делит небесную сферу на северное и южное полушария . ) равноденствий. В этих точках Солнце в своем видимом движении переходит соответственно из южного небесного полушария в северное (20 или 21 марта) и из северного полушария в южное (22 или 23 сентября).
) равноденствий. В этих точках Солнце в своем видимом движении переходит соответственно из южного небесного полушария в северное (20 или 21 марта) и из северного полушария в южное (22 или 23 сентября).
Только в дни равноденствий (два раза в году) лучи Солнца падают на Землю под прямым углом к оси ее вращения и поэтому только два раза в году день и ночь длятся по 12 часов (равноденствие), а все остальное время года или день короче ночи или наоборот . Причиной этого является то, что ось вращения Земли не перпендикулярна плоскости эклиптики, а наклонена к ней под углом 66,5° (рис. 2).
§ 2. Движение Луны вокруг Земли
Движение Луны вокруг Земли по ряду причин является весьма сложным. Если Землю принять за центр, то орбиту Луны в первом приближении можно считать эллипсом с эксцентриситетом
e = √ (a 2 — b 2) / a = 0,055 ,
где а и Ь — соответственно большая и малая полуоси эллипса. Когда Луна находится в наибольшей близости к Земле в перигее , ее расстояние от поверхности Земли составляет 356 400 км, в апогее это расстояние увеличивается до 406 700 км. Среднее же ее расстояние от Земли равно 384 000 км.
Среднее же ее расстояние от Земли равно 384 000 км.
Плоскость орбиты Луны наклонена к плоскости эклиптики под углом 5°09′; точки пересечения орбиты с эклиптикой называются узлами , а прямая, их соединяющая, — линией узлов . Линия узлов перемещается навстречу движению Луны, совершая полный оборот за 6793 суток, что составляет около 18,6 лет.
Промежуток времени между двумя последовательными прохождениями Луны через один и тот же узел называется драконическим месяцем ; его продолжительность равна 27,21 средних солнечных суток (см. § 5).
Поскольку линия узлов не остается на месте, Луна по истечении месяца не возвращается точно к своему первоначальному положению на орбите и каждое следующее обращение ее происходит по несколько иному пути.
По отношению к звездам полный оборот по своей орбите вокруг Земли Луна совершает за 27,32 средних солнечных суток. Этот промежуток времени называется сидерическим (иначе звездным ; sidus — по-латыни «звезда») месяцем; по прошествии этого месяца Луна возвращается к одной и той же звезде.
§ 3. Фазы Луны
Обращаясь вокруг Земли, Луна занимает различные положения относительно Солнца, и поскольку она представляет собой темное тело и светит лишь благодаря отражаемым ею солнечным лучам, то при разных положениях Луны относительно Солнца мы видим ее в разных фазах.
Рис. 3. Фазы Луны
Схематически лунные фазы показаны на рис. 3. На орбите изображена Луна (освещенная Солнцем наполовину) в различных положениях относительно Земли, а снаружи от орбиты показаны разные фазы Луны, как они видны с Земли.
Когда Луна при своем движении вокруг Земли окажется между Солнцем и Землей (положение 1 ), то к Земле будет обращена ее неосвещенная часть и в этом случае с Земли она не будет видна. Такая фаза Луны называется новолунием . Если Луна окажется в положении прямо противоположном Солнцу (положение 5 ), то часть ее, обращенная к Земле, будет полностью освещаться Солнцем, и Луна будет видна с Земли в виде полного диска. Эта фаза Луны называется полнолунием . Когда Луна окажется в положении 3 или 7 , то в это время направления на Солнце и Луну составят угол в 90° и поэтому с Земли будет видна только половина ее освещенного диска. Эти фазы Луны называются соответственно первой четвертью и последней четвертью .
Когда Луна окажется в положении 3 или 7 , то в это время направления на Солнце и Луну составят угол в 90° и поэтому с Земли будет видна только половина ее освещенного диска. Эти фазы Луны называются соответственно первой четвертью и последней четвертью .
Через два-три дня после новолуния Луна окажется в положении 2 , и тогда по вечерам при заходе Солнца будет видна освещенная часть лунного диска в виде узкого серпа. После первой четверти, по мере приближения Луны к полнолунию, которое наступает примерно через 15 суток после новолуния, освещенная часть ее с каждым днем будет увеличиваться, а после полнолуния размер освещенной части Луны, наоборот, будет постепенно уменьшаться, вплоть до следующего новолуния, когда она опять окажется полностью невидимой.
Для практических целей часто пользуются периодом повторения лунных фаз (например, от новолуния до новолуния). Этот период времени, называемый синодическим месяцем , составляет в среднем около 29,5 средних солнечных суток. Периодическую смену фаз Луны люди и использовали как вторую меру времени (после суток — периода оборота Земли вокруг своей оси), а именно месяц .
Периодическую смену фаз Луны люди и использовали как вторую меру времени (после суток — периода оборота Земли вокруг своей оси), а именно месяц .
В своем видимом суточном движении по небесной сфере любое небесное тело оказывается в высшей или низшей точке своего пути. Эти моменты называются кульминациями — соответственно верхней и нижней (про небесное тело говорят, что оно кульминирует ). В момент кульминации светило пересекает небесный меридиан — большой круг небесной сферы ZPVQZ»P»WQ» (рис. 1), плоскость которого проходит через ось мира РР» и отвесную линию.
Луна в течение месяца кульминирует в разные часы. В новолуние это происходит в 12 часов, в первой четверти — около 18 часов, в полнолуние — в 0 часов, а в последней четверти — в 6 часов.
Примечания:
Ленин В. И. Полн. собр. соч. — Т. 18.- С. 181.
Конечно, никакого небосвода на самом деле не существует, а его дневной голубой цвет обусловлен рассеянием солнечных лучей в атмосфере Земли.
В «Альмагесте» кроме описания мироздания содержится один из первых дошедших до нас звездных каталогов — список 1023 ярчайших звезд.
В астрономии по традиции большим кругом называют фактически окружность, плоскость которой проходит через центр небесной сферы.
Он отличается от видимого горизонта на земной поверхности, за который наблюдатель принимает линию пересечения небесного свода с ровной поверхностью Земли.
В каждом году самый короткий световой день и самая длинная ночь бывают 22 или 23 декабря (день зимнего солнцестояния). С этого времени световой день постепенно увеличивается («Солнце на летний путь выезжает», — говорили в народе).
Строго говоря, не Луна обращается вокруг Земли, а Земля и Луна обращаются вокруг общего центра тяжести, находящегося внутри Земли.
Как движется Луна? / Хабр
Светлой памяти моего учителя — первого декана физико-математического факультета Новочеркасского политехнического института, заведующего кафедрой «Теоретическая механика» Кабелькова Александра Николаевича
Август, лето подходит к концу. Народ яростно рванул на моря, да оно и неудивительно — самый сезон. А на Хабре, тем временем, буйным цветом распускается и пахнет лженаука. Если говорить о теме данного выпуска «Моделирования…», то в нем мы совместим приятное с полезным — продолжим обещанный цикл и совсем чуть-чуть поборемся с этой самой лженаукой за пытливые умы современной молодежи.
Народ яростно рванул на моря, да оно и неудивительно — самый сезон. А на Хабре, тем временем, буйным цветом распускается и пахнет лженаука. Если говорить о теме данного выпуска «Моделирования…», то в нем мы совместим приятное с полезным — продолжим обещанный цикл и совсем чуть-чуть поборемся с этой самой лженаукой за пытливые умы современной молодежи.
А вопрос ведь действительной не праздный — со школьных лет мы привыкли считать, что наш ближайший спутник в космическом пространстве — Луна движется вокруг Земли с периодом 29,5 суток, особенно не вдаваясь в сопутствующие подробности. На самом же деле наша соседка своеобразный и в какой-то степени уникальный астрономический объект, с движением которого вокруг Земли не всё так просто, как, возможно хотелось бы некоторым моим коллегам из ближайшего зарубежья.
Итак, оставив полемику в стороне, попытаемся с разных сторон, в меру своей компетенции, рассмотреть эту безусловно красивую, интересную и очень показательную задачу.
Открытый ещё во второй половине 17 века, сэром Исааком Ньютоном, закон всемирного тяготения говорит о том, что Луна притягивается к Земле (и Земля к Луне!) с силой, направленной вдоль прямой, соединяющей центры рассматриваемых небесных тел, и равной по модулю
где m1, m2 — массы, соответственно Луны и Земли; G = 6,67e-11 м3/(кг * с2) — гравитационная постоянная; r1,2 — расстояние между центрами Луны и Земли. Если принимать во внимание только эту силу, то, решив задачу о движении Луны как спутника Земли и научившись рассчитывать положение Луны на небе на фоне звезд, мы довольно скоро убедимся, путем прямых измерений экваториальных координат Луны, что в нашей консерватории не всё так гладко как хотелось бы. И дело здесь не в законе всемирного тяготения (а на ранних этапах развития небесной механики такие мысли высказывались весьма нередко), а в неучтенном возмущении движения Луны со стороны других тел. Каких? Смотрим на небо и наш взгляд сразу упирается в здоровенный, массой аж 1,99e30 килограмм плазменный шар прямо у нас под носом — Солнце. Луна притягивается к Солнцу? Ещё как, с силой, равной по модулю
Каких? Смотрим на небо и наш взгляд сразу упирается в здоровенный, массой аж 1,99e30 килограмм плазменный шар прямо у нас под носом — Солнце. Луна притягивается к Солнцу? Ещё как, с силой, равной по модулю
где m3 — масса Солнца; r1,3 — расстояние от Луны до Солнца. Сравним эту силу с предыдущей
Возьмем положение тел, в котором притяжение Луны к Солнцу будет минимальным: все три тела на одной прямой и Земля располагается между Луной и Солнцем. В этом случае наша формула примет вид:
где , м — среднее расстояние от Земли до Луны; , м — среднее расстояние от Земли до Солнца. Подставим в эту формулу реальные параметры
Вот это номер! Получается Луна притягивается к Солнцу силой, более чем в два раза превышающей силу её притяжения к Земле.
Подобное возмущение уже нельзя не учитывать и оно определенно повлияет на конечную траекторию движения Луны. Пойдем дальше, принимая во внимание допущение о том, что орбита Земли круговая с радиусом a, найдем геометрическое место точек вокруг Земли, где сила притяжения любого объекта к Земле равна силе его притяжения к Солнцу. Это будет сфера, с радиусом
Пойдем дальше, принимая во внимание допущение о том, что орбита Земли круговая с радиусом a, найдем геометрическое место точек вокруг Земли, где сила притяжения любого объекта к Земле равна силе его притяжения к Солнцу. Это будет сфера, с радиусом
смещенная вдоль прямой, соединяющей Землю и Солнце в сторону противоположенную направлению на Солнце на расстояние
где — отношение массы Земли к массе Солнца. Подставив численные значения параметров получим фактические размеры данной области: R = 259300 километров, и l = 450 километров. Эта сфера носит название сферы тяготения Земли относительно Солнца.
Известная нам орбита Луны лежит вне этой области. То есть в любой точке траектории Луна испытывает со стороны Солнца существенно большее притяжение, чем со стороны Земли.
Эта информация, часто порождает споры, о том, что Луна не спутник Земли, а самостоятельная планета Солнечной системы, орбита которой возмущена притяжением близкой Земли.
Оценим возмущение, вносимое Солнцем в траекторию Луны относительно Земли, а так же возмущение, вносимое Землей в траекторию Луны относительно Солнца, воспользовавшись критерием, предложенным П. Лапласом. Рассмотрим три тела: Солнце (S), Землю (E) и Луну (M).
Примем допущение, что орбиты Земли относительно Солнца и Луны относительно Земли являются круговыми.
Рассмотрим движение Луны в геоцентрической инерциальной системе отсчета. Абсолютное ускорение Луны в гелиоцентрической системе отсчета определяется действующими на неё силами тяготения и равно:
С другой стороны, в соответствии с теоремой Кориолиса, абсолютное ускорение Луны
где — переносное ускорение, равное ускорению Земли относительно Солнца; — ускорение Луны относительно Земли. Ускорения Кориолиса здесь не будет — выбранная нами система координат движется поступательно. Отсюда получаем ускорение Луны относительно Земли
Часть этого ускорения, равная обусловлена притяжением Луны к Земле и характеризует её невозмущенное геоцентрическое движение. Оставшаяся часть
Оставшаяся часть
ускорение Луны, вызванное возмущением со стороны Солнца.
Если рассматривать движение Луны в гелиоцентрической инерциальной системе отсчета, то всё намного проще, ускорение характеризует невозмущенное гелиоцентрическое движение Луны, а ускорение — возмущение этого движения со стороны Земли.
При существующих в текущую эпоху параметрах орбит Земли и Луны, в каждой точке траектории Луны справедливо неравенство
что можно проверить и непосредственным вычислением, но я сошлюсь на источник, дабы излишне не загромождать статью.
Что означает неравенство (1)? Да то, что в относительном выражении эффект от возмущения Луны Солнцем (причем очень существенно) меньше эффекта от притяжения Луны к Земле. И наоборот, возмущение Землей геолиоцентрической траектории Луны оказывает решающее влияние на характер её движения. Влияние земной гравитации в данном случае более существенно, а значит Луна «принадлежит» Земле по праву и является её спутником.
Интересным является другое — превратив неравенство (1) в уравнение можно найти геометрическое место точек, где эффекты возмущения Луны (да и любого другого тела) Землей и Солнцем одинаковы. К сожалению это у же не так просто, как в случае со сферой тяготения. Расчеты показывают, что данная поверхность описывается уравнением сумасшедшего порядка, но близка к эллипсоиду вращения. Всё что мы может сделать без лишних заморочек, это оценить общие габариты этой поверхности относительно центра Земли. Решая численно уравнение
относительно расстояния от центра Земли до искомой поверхности на достаточном количестве точек, получаем сечение искомой поверхности плоскостью эклиптики
Для наглядности здесь показаны и геоцентрическая орбита Луны и, найденная нами выше сфера тяготения Земли относительно Солнца. Из рисунка видно, что сфера влияния, или сфера гравитационного действия Земли относительно Солнца есть поверхность вращения относительно оси X, сплющенная вдоль прямой, соединяющей Землю и Солнце (вдоль оси затмений). Орбита Луны находится глубоко внутри этой воображаемой поверхности.
Орбита Луны находится глубоко внутри этой воображаемой поверхности.
Для практических расчетов данную поверхность удобно аппроксимировать сферой с центром в центра Земли и радиусом равным
где m — масса меньшего небесного тела; M — масса большего тела, в поле тяготения которого движется меньшее тело; a — расстояние между центрами тел. В нашем случае
Вот этот недоделанный миллион километров и есть тот теоретический предел, за который власть старушки Земли не распространяется — её влияние на траектории астрономических объектов настолько мало, что им можно пренебречь. А значит, запустить Луну по круговой орбите на расстоянии 38,4 млн. километров от Земли (как делают некоторые лингвисты) не получится, это физически невозможно.
Эта сфера, для сравнения, показана на рисунке синей пунктирной линией. При оценочных расчетах принято считать, что тело, находящееся внутри данной сферы будет испытывать тяготение исключительно со стороны Земли. Если тело находится снаружи данной сферы — считаем что тело движется в поле тяготения Солнца. В практической космонавтике известен метод сопряжения конических сечений, позволяющий приближенно рассчитать траекторию космического аппарата, используя решение задачи двух тел. При этом всё пространство, которое преодолевает аппарат разбивается на подобные сферы влияния.
Если тело находится снаружи данной сферы — считаем что тело движется в поле тяготения Солнца. В практической космонавтике известен метод сопряжения конических сечений, позволяющий приближенно рассчитать траекторию космического аппарата, используя решение задачи двух тел. При этом всё пространство, которое преодолевает аппарат разбивается на подобные сферы влияния.
Например, теперь понятно, для того чтобы иметь теоретическую возможность совершить маневры для выхода на окололунную орбиту, космический аппарат должен попасть внутрь сферы действия Луны относительно Земли. Её радиус легко рассчитать по формуле (3) и он равен 66 тысяч километров.
Таким образом, Луна справедливо может считаться спутником Земли. Однако, ввиду существенно влияния гравитационного поля Солнца она движется не в центральном гравитационном поле, а значит её траектория не является коническим сечением.
Итак, рассмотрим модельную задачу в общей постановке, известную в небесной механике как задача трех тел. Рассмотрим три тела произвольной массы, расположенных произвольным образом в пространстве и движущихся исключительно под действием сил взаимного гравитационного притяжения
Рассмотрим три тела произвольной массы, расположенных произвольным образом в пространстве и движущихся исключительно под действием сил взаимного гравитационного притяжения
Тела считаем материальными точками. Положение тел будем отсчитывать в произвольном базисе, с которым связана инерциальная система отсчета Oxyz. Положение каждого из тел задается радиус-вектором соответственно , и . На каждое тело действует сила гравитационного притяжения со стороны двух других тел, причем в соответствии с третьей аксиомой динамики точки (3-й закон Ньютона)
Запишем дифференциальные уравнения движения каждой точки в векторной форме
или, с учетом (4)
В соответствии с законом всемирного тяготения, силы взаимодействия направлены вдоль векторов
Вдоль каждого из этих векторов выпустим соответствующий орт
тогда каждая из гравитационных сил рассчитывается по формуле
С учетом всего этого система уравнений движения принимает вид
Введем обозначение, принятое в небесной механике
— гравитационный параметр притягивающего центра. Тогда уравнения движения примут окончательный векторный вид
Тогда уравнения движения примут окончательный векторный вид
Довольно популярным приемом при математическом моделировании является приведение дифференциальных уравнений и прочих соотношений, описывающих процесс, к безразмерным фазовым координатам и безразмерному времени. Нормируются так же и другие параметры. Это позволяет рассматривать, хоть и с применением численного моделирования, но в достаточно общем виде целый класс типовых задач. Вопрос о том, насколько это оправдано в каждой решаемой задаче оставляю открытым, но соглашусь, что в данном случае такой подход вполне справедлив.
Итак, введем некое абстрактное небесное тело с гравитационным параметром , такое, что период обращения спутника по эллиптической орбите с большой полуосью вокруг него равен . Все эти величины, в силу законов механики, связаны соотношением
Введем замену параметров. Для положения точек нашей системы
где — безразмерный радиус-вектор i-й точки;
для гравитационных параметров тел
где — безразмерный гравитационный параметр i-й точки;
для времени
где — безразмерное время.
Теперь пересчитаем ускорения точек системы через эти безразмерные параметры. Применим прямое двукратное дифференцирование по времени. Для скоростей
Для ускорений
При подстановке полученных соотношений в уравнения движения всё элегантно схлопывается в красивые уравнения:
Данная система уравнений до сих пор считается не интегрируемой в аналитических функциях. Почему считается а не является? Потому что успехи теории функции комплексного переменного привели к тому, что общее решение задачи трех тел таки появилось в 1912 году — Карлом Зундманом был найден алгоритм отыскания коэффициентов для бесконечных рядов относительно комплексного параметра, теоретически являющихся общим решением задачи трех тел. Но… для применения рядов Зундмана в практических расчетах с требуемой для них точностью требует получения такого числа членов этих рядов, что эта задача во много превосходит возможности вычислительных машин даже на сегодняшний день.
Поэтому численное интегрирование — единственный способ анализа решения уравнения (5)
Как я уже писал ранее, прежде чем начинать численное интегрирование, следует озаботится расчетом начальных условий для решаемой задачи. В рассматриваемой задаче поиск начальных условий превращается в самостоятельную подзадачу, так как система (5) дает нам девять скалярных уравнений второго порядка, что при переходе к нормальной форме Коши повышает порядок системы ещё в 2 раза. То есть нам необходимо рассчитать целых 18 параметров — начальные положения и компоненты начальной скорости всех точек системы. Где мы возьмем данные о положении интересующих нас небесных тел? Мы живем в мире, где человек ходил по Луне — естественно человечество должно обладать информацией, как эта самая Луна движется и где она находится.
То есть, скажете вы, ты, чувак, предлагаешь нам взять с полок толстые астрономические справочники, сдуть с них пыль… Не угадали! Я предлагаю сходить за этими данными к тем, кто собственно ходил по Луне, к NASA, а именно в Лабораторию реактивного движения, Пасадена, штат Калифорния. 2) 5.2 5.2 5.2
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 20:45:05 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Moon (301) {source: DE431mx}
Center body name: Earth (399) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : 6378.1 x 6378.
2) 5.2 5.2 5.2
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 20:45:05 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Moon (301) {source: DE431mx}
Center body name: Earth (399) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : 6378.1 x 6378. 1 x 6356.8 km {Equator, meridian, pole}
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 1.537109094089627E-03 Y =-2.237488447258137E-03 Z = 5.112037386426180E-06
VX= 4.593816208618667E-04 VY= 3.187527302531735E-04 VZ=-5.183707711777675E-05
LT= 1.567825598846416E-05 RG= 2.714605874095336E-03 RR=-2.707898607099066E-06
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.
1 x 6356.8 km {Equator, meridian, pole}
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 1.537109094089627E-03 Y =-2.237488447258137E-03 Z = 5.112037386426180E-06
VX= 4.593816208618667E-04 VY= 3.187527302531735E-04 VZ=-5.183707711777675E-05
LT= 1.567825598846416E-05 RG= 2.714605874095336E-03 RR=-2.707898607099066E-06
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000. 0
XY-plane: plane of the Earth’s orbit at the reference epoch
Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76)
X-axis : out along ascending node of instantaneous plane of the Earth’s
orbit and the Earth’s mean equator at the reference epoch
Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense
of Earth’s north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time
X X-component of position vector (au)
Y Y-component of position vector (au)
Z Z-component of position vector (au)
VX X-component of velocity vector (au/day)
VY Y-component of velocity vector (au/day)
VZ Z-component of velocity vector (au/day)
LT One-way down-leg Newtonian light-time (day)
RG Range; distance from coordinate center (au)
RR Range-rate; radial velocity wrt coord.
0
XY-plane: plane of the Earth’s orbit at the reference epoch
Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76)
X-axis : out along ascending node of instantaneous plane of the Earth’s
orbit and the Earth’s mean equator at the reference epoch
Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense
of Earth’s north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time
X X-component of position vector (au)
Y Y-component of position vector (au)
Z Z-component of position vector (au)
VX X-component of velocity vector (au/day)
VY Y-component of velocity vector (au/day)
VZ Z-component of velocity vector (au/day)
LT One-way down-leg Newtonian light-time (day)
RG Range; distance from coordinate center (au)
RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by …
Solar System Dynamics Group, Horizons On-Line Ephemeris System
4800 Oak Grove Drive, Jet Propulsion Laboratory
Pasadena, CA 91109 USA
Information: http://ssd.jpl.nasa.gov/
Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser)
http://ssd.jpl.nasa.gov/?horizons
telnet ssd.jpl.nasa.gov 6775 (via command-line)
Author : [email protected]
*******************************************************************************
center (au/day)
Geometric states/elements have no aberrations applied.
Computations by …
Solar System Dynamics Group, Horizons On-Line Ephemeris System
4800 Oak Grove Drive, Jet Propulsion Laboratory
Pasadena, CA 91109 USA
Information: http://ssd.jpl.nasa.gov/
Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser)
http://ssd.jpl.nasa.gov/?horizons
telnet ssd.jpl.nasa.gov 6775 (via command-line)
Author : [email protected]
*******************************************************************************
Бр-р-р, что это? Без паники, для того, кто хорошо учил в школе астрономию, механику и математику тут боятся нечего. Итак, самое главное конечное искомые координаты и компоненты скорости Луны.
$$SOE 2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB X = 1.537109094089627E-03 Y =-2.237488447258137E-03 Z = 5.112037386426180E-06 VX= 4.593816208618667E-04 VY= 3.187527302531735E-04 VZ=-5.183707711777675E-05 LT= 1.567825598846416E-05 RG= 2.714605874095336E-03 RR=-2.707898607099066E-06 $$EOE
Да-да-да, они декартовы! Если внимательно прочесть всю портянку, то мы узнаем, что начало этой системы координат совпадает с центром Земли. Плоскость XY лежит в плоскости земной орбиты (плоскости эклиптики) на эпоху J2000. Ось X направлена вдоль линии пересечения плоскости экватора Земли и эклиптики в точку весеннего равноденствия. Ось Z смотрит в направлении северного полюса Земли перпендикулярно плоскости эклиптики. Ну а ось Y дополняет всё это счастье до правой тройки векторов. По-умолчанию единицы измерения координат: астрономические единицы (умнички из NASA приводят и величину автрономической единицы в километрах). Единицы измерения скорости: астрономические единицы в день, день принимается равным 86400 секундам. Полный фарш!
Аналогичную информацию мы можем получить и для Земли
Полный вывод эфемерид Земли на 27. 2) = 1367.6 (mean), 1414 (perihelion), 1322 (aphelion)
ORBIT CHARACTERISTICS:
Obliquity to orbit, deg = 23.4392911 Sidereal orb period = 1.0000174 y
Orbital speed, km/s = 29.79 Sidereal orb period = 365.25636 d
Mean daily motion, deg/d = 0.9856474 Hill’s sphere radius = 234.9
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 21:16:21 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Earth (399) {source: DE431mx}
Center body name: Solar System Barycenter (0) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.
2) = 1367.6 (mean), 1414 (perihelion), 1322 (aphelion)
ORBIT CHARACTERISTICS:
Obliquity to orbit, deg = 23.4392911 Sidereal orb period = 1.0000174 y
Orbital speed, km/s = 29.79 Sidereal orb period = 365.25636 d
Mean daily motion, deg/d = 0.9856474 Hill’s sphere radius = 234.9
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 21:16:21 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Earth (399) {source: DE431mx}
Center body name: Solar System Barycenter (0) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0. 00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : (undefined)
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.755663665315949E-01 Y =-8.298818915224488E-01 Z =-5.366994499016168E-05
VX= 1.388633512282171E-02 VY= 9.678934168415631E-03 VZ= 3.429889230737491E-07
LT= 5.
00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : (undefined)
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.755663665315949E-01 Y =-8.298818915224488E-01 Z =-5.366994499016168E-05
VX= 1.388633512282171E-02 VY= 9.678934168415631E-03 VZ= 3.429889230737491E-07
LT= 5. 832932117417083E-03 RG= 1.009940888883960E+00 RR=-3.947237246302148E-05
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0
XY-plane: plane of the Earth’s orbit at the reference epoch
Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76)
X-axis : out along ascending node of instantaneous plane of the Earth’s
orbit and the Earth’s mean equator at the reference epoch
Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense
of Earth’s north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time
X X-component of position vector (au)
Y Y-component of position vector (au)
Z Z-component of position vector (au)
VX X-component of velocity vector (au/day)
VY Y-component of velocity vector (au/day)
VZ Z-component of velocity vector (au/day)
LT One-way down-leg Newtonian light-time (day)
RG Range; distance from coordinate center (au)
RR Range-rate; radial velocity wrt coord.
832932117417083E-03 RG= 1.009940888883960E+00 RR=-3.947237246302148E-05
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0
XY-plane: plane of the Earth’s orbit at the reference epoch
Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76)
X-axis : out along ascending node of instantaneous plane of the Earth’s
orbit and the Earth’s mean equator at the reference epoch
Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense
of Earth’s north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time
X X-component of position vector (au)
Y Y-component of position vector (au)
Z Z-component of position vector (au)
VX X-component of velocity vector (au/day)
VY Y-component of velocity vector (au/day)
VZ Z-component of velocity vector (au/day)
LT One-way down-leg Newtonian light-time (day)
RG Range; distance from coordinate center (au)
RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by …
Solar System Dynamics Group, Horizons On-Line Ephemeris System
4800 Oak Grove Drive, Jet Propulsion Laboratory
Pasadena, CA 91109 USA
Information: http://ssd.jpl.nasa.gov/
Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser)
http://ssd.jpl.nasa.gov/?horizons
telnet ssd.jpl.nasa.gov 6775 (via command-line)
Author : [email protected]
*******************************************************************************
center (au/day)
Geometric states/elements have no aberrations applied.
Computations by …
Solar System Dynamics Group, Horizons On-Line Ephemeris System
4800 Oak Grove Drive, Jet Propulsion Laboratory
Pasadena, CA 91109 USA
Information: http://ssd.jpl.nasa.gov/
Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser)
http://ssd.jpl.nasa.gov/?horizons
telnet ssd.jpl.nasa.gov 6775 (via command-line)
Author : [email protected]
*******************************************************************************
Здесь в качестве начала координат выбран барицентр (центр масс) Солнечной системы. Интересующие нас данные
$$SOE 2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB X = 5.755663665315949E-01 Y =-8.298818915224488E-01 Z =-5.366994499016168E-05 VX= 1.388633512282171E-02 VY= 9.678934168415631E-03 VZ= 3.429889230737491E-07 LT= 5.2) 5.2 5.2 5.2 ******************************************************************************* ******************************************************************************* Ephemeris / WWW_USER Wed Aug 15 21:19:24 2018 Pasadena, USA / Horizons ******************************************************************************* Target body name: Moon (301) {source: DE431mx} Center body name: Solar System Barycenter (0) {source: DE431mx} Center-site name: BODY CENTER ******************************************************************************* Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB Step-size : 0 steps ******************************************************************************* Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)} Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)} Center radii : (undefined) Output units : AU-D Output type : GEOMETRIC cartesian states Output format : 3 (position, velocity, LT, range, range-rate) Reference frame : ICRF/J2000.
0 Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch ******************************************************************************* JDTDB X Y Z VX VY VZ LT RG RR ******************************************************************************* $$SOE 2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB X = 5.771034756256845E-01 Y =-8.321193799697072E-01 Z =-4.855790760378579E-05 VX= 1.434571674368357E-02 VY= 9.997686898668805E-03 VZ=-5.149408819470315E-05 LT= 5.848610189172283E-03 RG= 1.012655462859054E+00 RR=-3.979984423450087E-05 $$EOE ******************************************************************************* Coordinate system description: Ecliptic and Mean Equinox of Reference Epoch Reference epoch: J2000.0 XY-plane: plane of the Earth's orbit at the reference epoch Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76) X-axis : out along ascending node of instantaneous plane of the Earth's orbit and the Earth's mean equator at the reference epoch Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense of Earth's north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]: JDTDB Julian Day Number, Barycentric Dynamical Time X X-component of position vector (au) Y Y-component of position vector (au) Z Z-component of position vector (au) VX X-component of velocity vector (au/day) VY Y-component of velocity vector (au/day) VZ Z-component of velocity vector (au/day) LT One-way down-leg Newtonian light-time (day) RG Range; distance from coordinate center (au) RR Range-rate; radial velocity wrt coord. center (au/day) Geometric states/elements have no aberrations applied. Computations by ... Solar System Dynamics Group, Horizons On-Line Ephemeris System 4800 Oak Grove Drive, Jet Propulsion Laboratory Pasadena, CA 91109 USA Information: http://ssd.
jpl.nasa.gov/ Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser) http://ssd.jpl.nasa.gov/?horizons telnet ssd.jpl.nasa.gov 6775 (via command-line) Author : [email protected] *******************************************************************************
$$SOE 2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB X = 5.771034756256845E-01 Y =-8.321193799697072E-01 Z =-4.855790760378579E-05 VX= 1.434571674368357E-02 VY= 9.997686898668805E-03 VZ=-5.149408819470315E-05 LT= 5.848610189172283E-03 RG= 1.012655462859054E+00 RR=-3.979984423450087E-05 $$EOE
Чудесно! Теперь необходимо слегка обработать полученные данные напильником.
Для начала определимся с масштабом, ведь наши уравнения движения (5) записаны в безразмерной форме. Данные, предоставленные NASA сами подсказывают нам, что за масштаб координат стоит взять одну астрономическую единицу. Соответственно в качестве эталонного тела, к которому мы будем нормировать массы других тел мы возьмем Солнце, а в качестве масштаба времени — период обращения Земли вокруг Солнца.
Соответственно в качестве эталонного тела, к которому мы будем нормировать массы других тел мы возьмем Солнце, а в качестве масштаба времени — период обращения Земли вокруг Солнца.
Все это конечно очень хорошо, но мы не задали начальные условия для Солнца. «Зачем?» — спросил бы меня какой-нибудь лингвист. А я бы ответил, что Солнце отнюдь не неподвижно, а тоже вращается по своей орбите вокруг центра масс Солнечной системы. В этом можно убедится, взглянув на данные NASA для Солнца
$$SOE 2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB X = 6.520050993518213E+04 Y = 1.049687363172734E+06 Z =-1.304404963058507E+04 VX=-1.265326939350981E-02 VY= 5.853475278436883E-03 VZ= 3.136673455633667E-04 LT= 3.508397935601254E+00 RG= 1.051791240756026E+06 RR= 5.053500842402456E-03 $$EOE
Взглянув на параметр RG мы увидим, что Солнце вращается вокруг барицентра Солнечной системы, и на 27.07.2018 центр звезды находится от него на расстоянии в миллион километров. Радиус Солнца, для справки — 696 тысяч километров. То есть барицентр Солнечной системы лежит в полумиллионе километров от поверхности светила. Почему? Да потому что все остальные тела, взаимодействующие с Солнцем так же сообщают ему ускорение, главным образом, конечно тяжеленький Юпитер. Соответственно у Солнца тоже есть своя орбита.
Радиус Солнца, для справки — 696 тысяч километров. То есть барицентр Солнечной системы лежит в полумиллионе километров от поверхности светила. Почему? Да потому что все остальные тела, взаимодействующие с Солнцем так же сообщают ему ускорение, главным образом, конечно тяжеленький Юпитер. Соответственно у Солнца тоже есть своя орбита.
Мы конечно можем выбрать эти данные в качестве начальных условий, но нет — мы же решаем модельную задачу трех тел, и Юпитер и прочие персонажи в неё не входят. Так что в ущерб реализму, зная положение и скорости Земли и Луны мы пересчитаем начальные условия для Солнца, так, чтобы центр масс системы Солнце — Земля — Луна находился в начале координат. Для центра масс нашей механической системы справедливо уравнение
Поместим центр масс в начало координат, то есть зададимся , тогда
откуда
Перейдем к безразмерным координатам и параметрам, выбрав
Дифференцируя (6) по времени и переходя к безразмерному времени получаем и соотношение для скоростей
где
Теперь напишем программу, которая сформирует начальные условия в выбранных нами «попугаях». На чем будем писать? Конечно же на Питоне! Ведь, как известно, это самый лучший язык для математического моделирования.
На чем будем писать? Конечно же на Питоне! Ведь, как известно, это самый лучший язык для математического моделирования.
Однако, если уйти от сарказма, то мы действительно попробуем для этой цели питон, а почему нет? Я обязательно приведу ссылку на весь код в моем профиле Github.
Расчет начальных условий для системы Луна — Земля — Солнце
#
# Исходные данные задачи
#
# Гравитационная постоянная
G = 6.67e-11
# Массы тел (Луна, Земля, Солнце)
m = [7.349e22, 5.792e24, 1.989e30]
# Расчитываем гравитационные параметры тел
mu = []
print("Гравитационные параметры тел")
for i, mass in enumerate(m):
mu.append(G * mass)
print("mu[" + str(i) + "] = " + str(mu[i]))
# Нормируем гравитационные параметры к Солнцу
kappa = []
print("Нормированные гравитационные параметры")
for i, gp in enumerate(mu):
kappa.append(gp / mu[2])
print("xi[" + str(i) + "] = " + str(kappa[i]))
print("\n")
# Астрономическая единица
a = 1.495978707e11
import math
# Масштаб безразмерного времени, c
T = 2 * math. pi * a * math.sqrt(a / mu[2])
print("Масштаб времени T = " + str(T) + "\n")
# Координаты NASA для Луны
xL = 5.771034756256845E-01
yL = -8.321193799697072E-01
zL = -4.855790760378579E-05
import numpy as np
xi_10 = np.array([xL, yL, zL])
print("Начальное положение Луны, а.е.: " + str(xi_10))
# Координаты NASA для Земли
xE = 5.755663665315949E-01
yE = -8.298818915224488E-01
zE = -5.366994499016168E-05
xi_20 = np.array([xE, yE, zE])
print("Начальное положение Земли, а.е.: " + str(xi_20))
# Расчитываем начальное положение Солнца, полагая что начало координат - в центре масс всей системы
xi_30 = - kappa[0] * xi_10 - kappa[1] * xi_20
print("Начальное положение Солнца, а.е.: " + str(xi_30))
# Вводим константы для вычисления безразмерных скоростей
Td = 86400.0
u = math.sqrt(mu[2] / a) / 2 / math.pi
print("\n")
# Начальная скорость Луны
vxL = 1.434571674368357E-02
vyL = 9.997686898668805E-03
vzL = -5.149408819470315E-05
vL0 = np.array([vxL, vyL, vzL])
uL0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vL0):
vL0[i] = v * a / Td
uL0[i] = vL0[i] / u
print("Начальная скорость Луны, м/с: " + str(vL0))
print(" -//- безразмерная: " + str(uL0))
# Начальная скорость Земли
vxE = 1.
pi * a * math.sqrt(a / mu[2])
print("Масштаб времени T = " + str(T) + "\n")
# Координаты NASA для Луны
xL = 5.771034756256845E-01
yL = -8.321193799697072E-01
zL = -4.855790760378579E-05
import numpy as np
xi_10 = np.array([xL, yL, zL])
print("Начальное положение Луны, а.е.: " + str(xi_10))
# Координаты NASA для Земли
xE = 5.755663665315949E-01
yE = -8.298818915224488E-01
zE = -5.366994499016168E-05
xi_20 = np.array([xE, yE, zE])
print("Начальное положение Земли, а.е.: " + str(xi_20))
# Расчитываем начальное положение Солнца, полагая что начало координат - в центре масс всей системы
xi_30 = - kappa[0] * xi_10 - kappa[1] * xi_20
print("Начальное положение Солнца, а.е.: " + str(xi_30))
# Вводим константы для вычисления безразмерных скоростей
Td = 86400.0
u = math.sqrt(mu[2] / a) / 2 / math.pi
print("\n")
# Начальная скорость Луны
vxL = 1.434571674368357E-02
vyL = 9.997686898668805E-03
vzL = -5.149408819470315E-05
vL0 = np.array([vxL, vyL, vzL])
uL0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vL0):
vL0[i] = v * a / Td
uL0[i] = vL0[i] / u
print("Начальная скорость Луны, м/с: " + str(vL0))
print(" -//- безразмерная: " + str(uL0))
# Начальная скорость Земли
vxE = 1. 388633512282171E-02
vyE = 9.678934168415631E-03
vzE = 3.429889230737491E-07
vE0 = np.array([vxE, vyE, vzE])
uE0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vE0):
vE0[i] = v * a / Td
uE0[i] = vE0[i] / u
print("Начальная скорость Земли, м/с: " + str(vE0))
print(" -//- безразмерная: " + str(uE0))
# Начальная скорость Солнца
vS0 = - kappa[0] * vL0 - kappa[1] * vE0
uS0 = - kappa[0] * uL0 - kappa[1] * uE0
print("Начальная скорость Солнца, м/с: " + str(vS0))
print(" -//- безразмерная: " + str(uS0))
388633512282171E-02
vyE = 9.678934168415631E-03
vzE = 3.429889230737491E-07
vE0 = np.array([vxE, vyE, vzE])
uE0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vE0):
vE0[i] = v * a / Td
uE0[i] = vE0[i] / u
print("Начальная скорость Земли, м/с: " + str(vE0))
print(" -//- безразмерная: " + str(uE0))
# Начальная скорость Солнца
vS0 = - kappa[0] * vL0 - kappa[1] * vE0
uS0 = - kappa[0] * uL0 - kappa[1] * uE0
print("Начальная скорость Солнца, м/с: " + str(vS0))
print(" -//- безразмерная: " + str(uS0))
Выхлоп программы
Гравитационные параметры тел mu[0] = 4901783000000.0 mu[1] = 386326400000000.0 mu[2] = 1.326663e+20 Нормированные гравитационные параметры xi[0] = 3.6948215183509304e-08 xi[1] = 2.912016088486677e-06 xi[2] = 1.0 Масштаб времени T = 31563683.35432583 Начальное положение Луны, а.е.: [ 5.77103476e-01 -8.32119380e-01 -4.85579076e-05] Начальное положение Земли, а.е.: [ 5.75566367e-01 -8.29881892e-01 -5.36699450e-05] Начальное положение Солнца, а.е.: [-1.69738146e-06 2.44737475e-06 1.58081871e-10] Начальная скорость Луны, м/с: [24838.98933473 17310.56333294 -89.15979106] -//- безразмерная: [ 5.24078311 3.65235907 -0.01881184] Начальная скорость Земли, м/с: [2.40435899e+04 1.67586567e+04 5.93870516e-01] -//- безразмерная: [5.07296163e+00 3.53591219e+00 1.25300854e-04] Начальная скорость Солнца, м/с: [-7.09330769e-02 -4.94410725e-02 1.56493465e-06] -//- безразмерная: [-1.49661835e-05 -1.04315813e-05 3.30185861e-10]
Собственно само интегрирование сводится к более-менее стандартной для SciPy процедуре подготовки системы уравнений: преобразованию системы ОДУ к форме Коши и вызову соответствующих функций-решателей. Для преобразования системы к форме Коши вспоминаем, что
Тогда введя вектор состояния системы
сводим (7) и (5) к одному векторному уравнению
Для интегрирования (8) с имеющимися начальными условиями напишем немного, совсем немного кода
Интегрирования уравнений движения в задаче трех тел
#
# Вычисление векторов обобщенных ускорений
#
def calcAccels(xi):
k = 4 * math. pi ** 2
xi12 = xi[1] - xi[0]
xi13 = xi[2] - xi[0]
xi23 = xi[2] - xi[1]
s12 = math.sqrt(np.dot(xi12, xi12))
s13 = math.sqrt(np.dot(xi13, xi13))
s23 = math.sqrt(np.dot(xi23, xi23))
a1 = (k * kappa[1] / s12 ** 3) * xi12 + (k * kappa[2] / s13 ** 3) * xi13
a2 = -(k * kappa[0] / s12 ** 3) * xi12 + (k * kappa[2] / s23 ** 3) * xi23
a3 = -(k * kappa[0] / s13 ** 3) * xi13 - (k * kappa[1] / s23 ** 3) * xi23
return [a1, a2, a3]
#
# Система уравнений в нормальной форме Коши
#
def f(t, y):
n = 9
dydt = np.zeros((2 * n))
for i in range(0, n):
dydt[i] = y[i + n]
xi1 = np.array(y[0:3])
xi2 = np.array(y[3:6])
xi3 = np.array(y[6:9])
accels = calcAccels([xi1, xi2, xi3])
i = n
for accel in accels:
for a in accel:
dydt[i] = a
i = i + 1
return dydt
# Начальные условия задачи Коши
y0 = [xi_10[0], xi_10[1], xi_10[2],
xi_20[0], xi_20[1], xi_20[2],
xi_30[0], xi_30[1], xi_30[2],
uL0[0], uL0[1], uL0[2],
uE0[0], uE0[1], uE0[2],
uS0[0], uS0[1], uS0[2]]
#
# Интегрируем уравнения движения
#
# Начальное время
t_begin = 0
# Конечное время
t_end = 30.
pi ** 2
xi12 = xi[1] - xi[0]
xi13 = xi[2] - xi[0]
xi23 = xi[2] - xi[1]
s12 = math.sqrt(np.dot(xi12, xi12))
s13 = math.sqrt(np.dot(xi13, xi13))
s23 = math.sqrt(np.dot(xi23, xi23))
a1 = (k * kappa[1] / s12 ** 3) * xi12 + (k * kappa[2] / s13 ** 3) * xi13
a2 = -(k * kappa[0] / s12 ** 3) * xi12 + (k * kappa[2] / s23 ** 3) * xi23
a3 = -(k * kappa[0] / s13 ** 3) * xi13 - (k * kappa[1] / s23 ** 3) * xi23
return [a1, a2, a3]
#
# Система уравнений в нормальной форме Коши
#
def f(t, y):
n = 9
dydt = np.zeros((2 * n))
for i in range(0, n):
dydt[i] = y[i + n]
xi1 = np.array(y[0:3])
xi2 = np.array(y[3:6])
xi3 = np.array(y[6:9])
accels = calcAccels([xi1, xi2, xi3])
i = n
for accel in accels:
for a in accel:
dydt[i] = a
i = i + 1
return dydt
# Начальные условия задачи Коши
y0 = [xi_10[0], xi_10[1], xi_10[2],
xi_20[0], xi_20[1], xi_20[2],
xi_30[0], xi_30[1], xi_30[2],
uL0[0], uL0[1], uL0[2],
uE0[0], uE0[1], uE0[2],
uS0[0], uS0[1], uS0[2]]
#
# Интегрируем уравнения движения
#
# Начальное время
t_begin = 0
# Конечное время
t_end = 30. 7 * Td / T;
# Интересующее нас число точек траектории
N_plots = 1000
# Шаг времени между точкими
step = (t_end - t_begin) / N_plots
import scipy.integrate as spi
solver = spi.ode(f)
solver.set_integrator('vode', nsteps=50000, method='bdf', max_step=1e-6, rtol=1e-12)
solver.set_initial_value(y0, t_begin)
ts = []
ys = []
i = 0
while solver.successful() and solver.t <= t_end:
solver.integrate(solver.t + step)
ts.append(solver.t)
ys.append(solver.y)
print(ts[i], ys[i])
i = i + 1
7 * Td / T;
# Интересующее нас число точек траектории
N_plots = 1000
# Шаг времени между точкими
step = (t_end - t_begin) / N_plots
import scipy.integrate as spi
solver = spi.ode(f)
solver.set_integrator('vode', nsteps=50000, method='bdf', max_step=1e-6, rtol=1e-12)
solver.set_initial_value(y0, t_begin)
ts = []
ys = []
i = 0
while solver.successful() and solver.t <= t_end:
solver.integrate(solver.t + step)
ts.append(solver.t)
ys.append(solver.y)
print(ts[i], ys[i])
i = i + 1
Посмотрим что у нас получилось. Получилась пространственная траектория Луны на первые 29 суток от выбранной нами начальной точки
а так же её проекция в плоскость эклиптики.
«Эй, дядя, что ты нам впариваешь?! Это же окружность!».
Во-первых, таки не окружность — заметно смещение проекции траектории от начала координат вправо и вниз. Во-вторых — ничего не замечаете? Не, ну правда?
Обещаю подготовить обоснование того (на основе анализа погрешностей счета и данных NASA), что полученное смещение траектории не есть следствие ошибок интегрирования. Пока предлагаю читателю поверить мне на слово — это смещение есть следствие солнечного возмущения лунной траектории. Крутанем-ка еще один оборот
Пока предлагаю читателю поверить мне на слово — это смещение есть следствие солнечного возмущения лунной траектории. Крутанем-ка еще один оборот
Во как! Причем обратите внимание на то, что исходя из начальных данных задачи Солнце находится как раз в той стороне, куда смещается траектория Луны на каждом обороте. Да это наглое Солнце ворует у нас наш любимый спутник! Ох уж это Солнце!
Можно сделать вывод, что солнечная гравитация влияет на орбиту Луны достаточно существенно — старушка не ходит по небу дважды одним и тем же путём. Картинка за полгода движения позволяет (по крайней мере качественно) убедится в этом (картинка кликабельна)
Интересно? Ещё бы. Астрономия вообще наука занятная.
В вузе, где я учился и работал без малого семь лет — Новочеркасском политехе — ежегодно проводилась зональная олимпиада студентов по теоретической механике вузов Северного Кавказа. Трижды мы принимали и Всероссийскую олимпиаду. На открытии, наш главный «олимпиец», профессор Кондратенко А.И., всегда говорил: «Академик Крылов называл механику поэзией точных наук».
На открытии, наш главный «олимпиец», профессор Кондратенко А.И., всегда говорил: «Академик Крылов называл механику поэзией точных наук».
Я люблю механику. Всё то хорошее, чего я добился в своей жизни и карьере произошло благодаря этой науке и моим замечательным учителям. Я уважаю механику.
Поэтому, я никогда не позволю издеваться над этой наукой и нагло эксплуатировать её в своих целях никому, будь он хоть трижды доктор наук и четырежды лингвист, и разработал хоть миллион учебных программ. Я искренне считаю, что написание статей на популярном публичном ресурсе должно предусматривать их тщательную вычитку, нормальное оформление (формулы LaTeX — это не блажь разработчиков ресурса!) и отсутствие ошибок, приводящих к результатам нарушающим законы природы. Последнее вообще «маст хэв».
Я часто говорю своим студентам: «компьютер освобождает ваши руки, но это не значит, что при этом нужно отключать и мозг».
Ценить и уважать механику я призываю и вас, мои уважаемые читатели. Охотно отвечу на любые вопросы, а исходный текст примера решения задачи трех тел на языке Python, как и обещал, выкладываю в своем профиле Github.
Охотно отвечу на любые вопросы, а исходный текст примера решения задачи трех тел на языке Python, как и обещал, выкладываю в своем профиле Github.
Спасибо за внимание!
Лунный тормоз
Лев Асламазов
«Квант» №1, 2020
Впервые опубликовано в «Кванте» №8 за 1987 год.
Издавна люди считали, что морские приливы связаны с Луной. Луна притягивает воду Мирового океана, и в том месте океана, над которым находится Луна, образуется водяной «горб». Горб «стоит» под Луной, а Земля вращается вокруг своей оси; поднявшаяся вода «наползает» на берег — наступает прилив, вода отступает — отлив. Казалось бы, такое объяснение выглядит вполне естественно. Однако признать его удовлетворительным нельзя: из него следует, что приливы должны наблюдаться один раз в сутки, а в действительности они бывают каждые 12 часов, т.е. два раза в сутки.
Первую теорию приливов, объясняющую это явление, создал Ньютон вскоре после открытия закона всемирного тяготения. В океане действительно образуются два горба: один — у ближайшей к Луне поверхности воды, а другой — с противоположной стороны Земли (рис. 1). Обсудим подробнее причину возникновения второго горба.
1). Обсудим подробнее причину возникновения второго горба.
Мы привыкли говорить, что Луна вращается вокруг Земли. На самом же деле и Луна и Земля вращаются вокруг общего центра. Если бы этого вращения не было, то под действием силы притяжения Луна упала бы на Землю (точнее, Земля и Луна упали бы друг на друга — ведь Луна тоже притягивает Землю). Как же происходит это вращение? Представим себе, что массы Земли и Луны одинаковы. Тогда они будут двигаться вокруг точки, которая лежит на середине отрезка, соединяющего их центры. Теперь давайте мысленно «наращивать» массу Земли. Тогда центр вращения будет смещаться в сторону Земли. Поскольку масса Земли гораздо больше массы Луны (в 81 раз), то центр вращения C оказывается лежащим внутри земного шара (но он обязательно смещен относительно центра Земли O).
Это вращение существенно влияет на картину приливов. Вода отступает от центра вращения. (Нечто подобное происходит в стакане воды, когда, размешивая воду ложкой, вы приводите ее во вращение, — вода отходит от центра стакана и поднимается у краев. ) На дальней от Луны стороне Земли, где наименьшая сила притяжения, образуется водяной горб.
) На дальней от Луны стороне Земли, где наименьшая сила притяжения, образуется водяной горб.
Конечно, приведенное нами объяснение приливов является весьма упрощенным. Мы не принимали во внимание неравномерность распределения воды по поверхности Земли, не учитывали влияния сил притяжения к Солнцу и других факторов, способных существенно изменить описанную картину. Однако ответ на главный вопрос мы получили: притяжение к Луне и вращение Земли вокруг общего с Луной центра C приводят к образованию двух приливных горбов в океане.
А теперь самое время объяснить принцип действия лунного тормоза. Оказывается, что водяные горбы находятся не на линии, соединяющей центры Земли и Луны (как для простоты показано на рисунке 1), а несколько смещены в сторону (рис. 2). Происходит это по следующей причине. Земля, вращаясь вокруг своей оси, увлекает за собой и воду в океане (это происходит потому, что существует трение). В результате этого по мере поворота Земли в приливные горбы должны вовлекаться все новые и новые массы воды. Деформация, однако, всегда запаздывает по отношению к вызывающей ее силе (ведь сила создает ускорение, и должно пройти какое-то время, чтобы частицы приобрели скорость и сместились на заметные расстояния). Поэтому точка максимального поднятия воды (вершина горба) и точка на линии центров, где на воду действует максимальная сила притяжения к Луне, не совпадают. Образование горба происходит с некоторым запаздыванием, и он смещается в сторону вращения Земли. А в таком случае, как видно из рисунка 2, сила притяжения Луны к воде уже не проходит через центр собственного вращения Земли и как бы стремится «повернуть» ее в противоположную сторону, иными словами — тормозит ее вращение. Длительность суток каждодневно увеличивается!
Деформация, однако, всегда запаздывает по отношению к вызывающей ее силе (ведь сила создает ускорение, и должно пройти какое-то время, чтобы частицы приобрели скорость и сместились на заметные расстояния). Поэтому точка максимального поднятия воды (вершина горба) и точка на линии центров, где на воду действует максимальная сила притяжения к Луне, не совпадают. Образование горба происходит с некоторым запаздыванием, и он смещается в сторону вращения Земли. А в таком случае, как видно из рисунка 2, сила притяжения Луны к воде уже не проходит через центр собственного вращения Земли и как бы стремится «повернуть» ее в противоположную сторону, иными словами — тормозит ее вращение. Длительность суток каждодневно увеличивается!
«Лунный тормоз» безотказно работает уже многие миллионы лет. У окаменевших кораллов, живших в океане около 400 миллионов лет назад, ученые обнаружили структуры, связанные с суточным и годичным ростом кораллов. Структуры эти назвали суточными и годичными кольцами. Когда кольца подсчитали, то оказалось, что на каждый год приходится 395 суточных колец. Продолжительность года, т.е. времени, за которое Земля совершает полный оборот вокруг Солнца, с тех пор, по-видимому, не изменилась. Значит, тогда — 400 миллионов лет назад — в сутках было только 22 часа!
Когда кольца подсчитали, то оказалось, что на каждый год приходится 395 суточных колец. Продолжительность года, т.е. времени, за которое Земля совершает полный оборот вокруг Солнца, с тех пор, по-видимому, не изменилась. Значит, тогда — 400 миллионов лет назад — в сутках было только 22 часа!
Лунный тормоз продолжает работать и сейчас, увеличивая длительность суток. К чему это может привести в отдаленном будущем? В конце концов время обращения Земли вокруг своей оси может сравняться со временем обращения Луны вокруг Земли, и тогда торможение прекратится. Земля будет обращена к Луне всегда одной стороной, точно так же, как обращена к нам одной стороной Луна (попробуйте сами объяснить, почему это произошло). Длительность суток на Земле увеличится, и в результате может измениться климат. Земля будет долго оставаться обращенной к Солнцу одной стороной, а на другой стороне в это время будет господствовать долгая ночь. Горячий воздух с нагретой стороны с огромной скоростью устремится к холодной, на Земле задуют сильные ветры, поднимутся песчаные бури. ..
..
Но такой прогноз может и не сбыться — ведь эти возможные времена столь далеки, что предсказать все изменения, которые произойдут в системе Земля — Луна — Солнце, просто невозможно. А если такая картина и окажется реальной, то люди обязательно придумают, как предотвратить бедствие.
Спутник Луна
Общие сведения о Луне
Луна – это единственный естественный спутник Земли.
Луна является наиболее близким к Солнцу спутником планеты, поскольку у Меркурия и Венеры нет спутников.
Луна состоит из коры, верхней мантии (астеносферы), средней мантии, нижней мантии и ядра.
Поверхность Луны покрыта реголитом – смесью тонкой пыли и скалистых обломков, образующихся в результате столкновений метеоритов с лунной поверхностью.
Русское наименование Луна восходит к праславянскому «светлая». Греки называли спутник Земли Селеной, древние египтяне – Ях (Иях), вавилоняне – Син.
В 1984 году на Гавайской конференции по планетологии была коллективно выдвинута теория возникновения Луны, получившая название теории Гигантского столкновения. Она утверждает, что спутник возник 4,6 миллиарда лет назад после столкновения Земли с небесным телом Тейа.
Она утверждает, что спутник возник 4,6 миллиарда лет назад после столкновения Земли с небесным телом Тейа.
Орбита Луны
Перигей (ближайшая к Земле точка орбиты): 363 104 километра (изменяется в пределах 356 400 – 370 400 километров).
Апогей (самая далекая от Земли точка орбиты): 405 696 километров (изменяется в пределах 404 000 – 406 700 километров).
Средняя скорость движения Луны по орбите составляет около 1,023 километра в секунду.
Луна вращается вокруг Земли по эллиптической орбите с периодом 27,32166 суток, постепенно удаляясь от нее вследствие приливного ускорения на 38 миллиметров в год, то есть ее орбита представляет собой медленно раскручивающуюся спираль.
3D-модель Луны
Физические характеристики Луны
Луна – пятый по размеру спутник Солнечной системы.
Температура поверхности Луны колеблется от −173 °C ночью до +127 °C в подсолнечной точке. Температура пород на глубине 1 метр постоянна и равна −35 °C.
Средний радиус Луны составляет 1737,1 километра, то есть примерно 0,273 радиуса Земли.
Площадь поверхности Луны составляет 3,793 х 107 квадратных километров.
Средняя плотность Луны составляет 3,3464 грамм на кубический сантиметр.
Ускорение свободного падения на Луне равно 1,62 метра на секунду в квадрате (0,165 g).
Масса Луны равна 7,3477 х 1022 килограмм.
Сравнительные размеры Земли и Луны
Атмосфера Луны
Атмосфера Луны крайне разрежена, в ней присутствуют следы водорода, гелия, неона и аргона.
Когда поверхность не освещена Солнцем, содержание газов над ней не превышает 2 x 105 частиц на кубический сантиметр, а после восхода увеличивается на два порядка за счет дегазации грунта.
Исследование Луны
Уже во II веке до н. э. Гиппарх исследовал движение Луны по звездному небу, определив наклон лунной орбиты относительно эклиптики, размеры Луны и расстояние от Земли, а также выявил ряд особенностей движения.
Одну из первых лунных карт составил Джованни Риччиоли в 1651 году, он же дал названия крупным темным областям, именовав их «морями».
Новым этапом исследования Луны стало применение фотографии в астрономических наблюдениях, начиная с середины XIX века.
Впервые Луны достиг советский космический корабль «Луна-2» 13 сентября 1959 года.
Впервые удалось заглянуть на обратную сторону Луны в 1959 году, когда советская станция «Луна-3» пролетела над ней и сфотографировала невидимую с Земли часть ее поверхности.
Американская программа пилотируемого полета на Луну называлась «Apollo». Первая посадка произошла 20 июля 1969 года; последняя – в декабре 1972 года. Первым человеком, ступившим 21 июля 1969 года на поверхность Луны, стал американец Нил Армстронг, вторым – Эдвин Олдрин. Третий член экипажа Майкл Коллинз оставался в орбитальном модуле.
После того как в августе 1976 года советская станция «Луна-24» доставила на Землю образцы лунного грунта, следующий аппарат – японский спутник «Hiten» – полетел к Луне лишь в 1990 году.
В рамках исследования Луны в настоящее время работают несколько луноходов и орбитальных зондов разных государств.
Интересные факты о Луне
Луна является единственным внеземным астрономическим объектом, на котором побывал человек.
Юридический статус Луны описывает Соглашение о Луне от 1979 года, которое провозглашает принцип исключительно мирного использования Луны и других небесных тел, принцип равных прав всех государств на исследования небесных тел, принцип недопустимости претензии со стороны любого государства на распространение своего суверенитета на какое-либо небесное тело.
Земной диск висит в небе Луны почти неподвижно.
Гравитационное влияние Луны вызывает на Земле морские приливы и отливы. Максимальная амплитуда приливной волны на Земле наблюдается в заливе Фанди в Канаде и составляет 18 метров.
Хотя Луна и вращается вокруг своей оси, она всегда обращена к Земле одной и той же стороной, то есть обращение Луны вокруг Земли и вращение вокруг собственной оси синхронизировано.
Явление либрации, открытое Галилео Галилеем в 1635 году, позволяет наблюдать около 59 % лунной поверхности.
В отличие от Земли Луна не имеет глобального магнитного поля, однако намагниченные породы на ее поверхности создают небольшие локализованные защитные экраны.
Суперлуние – астрономическое явление, при котором момент прохождения Луной перигея совпадает с ее полной фазой.
Фотографии Луны
Снимок вспышки на Луне, произошедшей во время полного затмения 21 января 2019 года
Луна и Международная космическая станция
Радиоволны Млечного Пути, отраженные от поверхности Луны
Один из «солнечных ожогов» на Луне
Земля с орбиты Луны
Транзит Луны по диску Солнца
Астронавт миссии «Апполон-17» Юджин Сернан во время тест-драйва «лунного ровера»
Суперлуние в Санкт-Петербурге
Карта Луны, созданная рукой английского художника Джона Рассела на закате XVIII века
Последние новости о Луне
Наверх
Иллюзия осевого вращения Луны. Н.Тесла
«Electrical Experimenter», февраль, 1919 г. Знаменитые научные заблуждения.
Автор Никола Тесла
С тех пор как Галилей сделал свое открытие, общеизвестным стал факт, что Луна, перемещаясь в пространстве, всегда обращена к земле одной стороной. Это объясняется тем, что, делая один оборот вокруг своей планеты-матери, Луна совершает только один оборот вокруг своей оси. Вращательное движение небесного тела должно подвергаться изменениям с течением времени: или замедляться под влиянием сопротивления, внутреннего или внешнего, или ускоряться вследствие сжатия или других причин. Неизменная скорость вращения на протяжении всех фаз космической эволюции явно невозможна. В таком случае это просто чудо, что в данный момент своего долгого существования наш спутник должен вращаться именно так — не быстрее и не медленнее. Однако многие астрономы признают как доказанный факт, что такое вращение имеет место. В действительности этого нет, есть только видимость, это иллюзия, к тому же весьма удивляющая.
Я постараюсь разъяснить это, прибегнув к иллюстрации 1, в которой Е — Земля, а М — Луна. Луна перемещается в космическом пространстве так, как показывает стрелка, нанесенная на нее, и всегда занимает указанную позицию относительно Земли. Если кто-либо сможет представить, что он смотрит вниз на орбитальную плоскость и отслеживает движение, он уверится, что Луна и вправду вращается на своей оси, совершая оборот вокруг Земли. Вот здесь-то наблюдатель и допустит ошибку. Чтобы он окончательно убедился в своем заблуждении, возьмем шайбу, таким же образом отмеченную, и, прижимая центр шайбы так, чтобы она могла вращаться, будем перемещать ее вокруг неподвижного объекта, всё время удерживая стрелку направленной на этот объект. Несмотря на то что, согласно его личному зрительному восприятию, диск будет вращаться на своей оси, такого вращения нет в природе. Наблюдатель сможет тотчас же рассеять эту иллюзию, удерживая шайбу в фиксированном состоянии и одновременно перемещая ее по кругу. Теперь он без труда заметит, что предполагаемое осевое вращение лишь кажущееся, это лишь впечатление, создаваемое последовательными изменениями положения в пространстве.
Луна перемещается в космическом пространстве так, как показывает стрелка, нанесенная на нее, и всегда занимает указанную позицию относительно Земли. Если кто-либо сможет представить, что он смотрит вниз на орбитальную плоскость и отслеживает движение, он уверится, что Луна и вправду вращается на своей оси, совершая оборот вокруг Земли. Вот здесь-то наблюдатель и допустит ошибку. Чтобы он окончательно убедился в своем заблуждении, возьмем шайбу, таким же образом отмеченную, и, прижимая центр шайбы так, чтобы она могла вращаться, будем перемещать ее вокруг неподвижного объекта, всё время удерживая стрелку направленной на этот объект. Несмотря на то что, согласно его личному зрительному восприятию, диск будет вращаться на своей оси, такого вращения нет в природе. Наблюдатель сможет тотчас же рассеять эту иллюзию, удерживая шайбу в фиксированном состоянии и одновременно перемещая ее по кругу. Теперь он без труда заметит, что предполагаемое осевое вращение лишь кажущееся, это лишь впечатление, создаваемое последовательными изменениями положения в пространстве.
Но можно получить более убедительные доказательства того, что Луна не вращается и не может вращаться вокруг своей оси. С этой целью обратим внимание на иллюстрацию 2, где и спутник М1 и Земля Е представлены помещенными в однородную массу М1, обозначенную точечным пунктиром, которая должна вращаться, чтобы сообщить Луне ее естественную поступательную скорость. Очевидно, что, если бы лунный шар мог вращаться, как все считают, это было бы в той же степени верно для любой другой части массы М1,например, для сферы М2 , обозначенной пунктиром, и тогда часть, общая для обоих тел, должна будет вращаться одновременно во встречных направлениях. Это можно проиллюстрировать экспериментально предложенным выше способом, используя вместо одной две перекрывающие одна другую вращающиеся шайбы, что можно легко представить в виде кругов М и М2 и перемещать их вокруг центра Е так, чтобы сплошные и пунктирные стрелки всегда указывали на этот центр. Нет необходимости приводить какие-либо дополнительные доводы, чтобы доказать, что два круговых движения не могут сосуществовать, их невозможно даже представить в воображении и согласовать чисто теоретически.
Нет необходимости приводить какие-либо дополнительные доводы, чтобы доказать, что два круговых движения не могут сосуществовать, их невозможно даже представить в воображении и согласовать чисто теоретически.
Дело в том, что так называемое «осевое вращение» луны есть явление обманчивое, вводящее в заблуждение как зрение, так и сознание, оно лишено физического смысла. Оно не имеет ничего общего с подлинным вращением массы, которому свойственны определенные и несомненные характеристики. Уже написаны тома на эту тему и выдвинуто много ложных аргументов в поддержку этого заблуждения. В результате делается вывод, что если бы Луна не вращалась на своей оси, она выставляла бы на земное обозрение всю поверхность, а поскольку видна половина, она должна вращаться. Первое утверждение верно, но логика второго ущербна, так как она допускает лишь одну альтернативу. Вывод не имеет под собой оснований, поскольку такой же результат можно получить и другим способом. Луна всё-таки вращается, но не самостоятельно, а вокруг оси, проходящей через центр земли — этот вывод истинный и единственный.
Оно не имеет ничего общего с подлинным вращением массы, которому свойственны определенные и несомненные характеристики. Уже написаны тома на эту тему и выдвинуто много ложных аргументов в поддержку этого заблуждения. В результате делается вывод, что если бы Луна не вращалась на своей оси, она выставляла бы на земное обозрение всю поверхность, а поскольку видна половина, она должна вращаться. Первое утверждение верно, но логика второго ущербна, так как она допускает лишь одну альтернативу. Вывод не имеет под собой оснований, поскольку такой же результат можно получить и другим способом. Луна всё-таки вращается, но не самостоятельно, а вокруг оси, проходящей через центр земли — этот вывод истинный и единственный.
Несомненно безошибочным доказательством вращения массы является наличие энергии движения. Луна не обладает кинетической энергией такого рода. Если бы это имело место, то вращающееся тело, пусть это будет М1, содержало бы механическую энергию, отличную от той, о которой мы имеем экспериментальное подтверждение. Вне зависимости от этого совмещение между осевым и орбитальным периодами само по себе является в высшей степени невероятным, поскольку это не перманентное состояние, к которому стремится система. Любое осевое вращение, предоставленное само себе, замедляется под воздействием сил, внешних или внутренних, и должно прекратиться. Даже если допустить, что оно полностью управляется приливно-отливными движениями океана, такое совпадение было бы поразительным. Но если мы вспомним, что большинство спутников обнаруживают это характерное свойство, вероятность совпадения становится бесконечно малой.
Вне зависимости от этого совмещение между осевым и орбитальным периодами само по себе является в высшей степени невероятным, поскольку это не перманентное состояние, к которому стремится система. Любое осевое вращение, предоставленное само себе, замедляется под воздействием сил, внешних или внутренних, и должно прекратиться. Даже если допустить, что оно полностью управляется приливно-отливными движениями океана, такое совпадение было бы поразительным. Но если мы вспомним, что большинство спутников обнаруживают это характерное свойство, вероятность совпадения становится бесконечно малой.
Были выдвинуты три теории относительно происхождения Луны. Согласно самой ранней, предложенной великим немецким философом Кантом и развитой Лапласом в его монументальном трактате «Небесная механика», планеты выбрасываются из более обширных серединных масс центробежной силой. Почти сорок лет тому назад профессор Джордж Г. Дарвин в мастерски написанном реферате о приливно-отливном трении представил математические доказательства, считающиеся неопровержимыми, что Луна отделилась от Земли. В последнее время эта признанная теория подвергается критике со стороны профессора т. Дж. Дж. Си в его выдающемся труде «Эволюция звёздных систем», в котором он утверждает, что центробежная сила совершенно недостаточна, чтобы осуществить отделение, и что все планеты, включая Луну, зарождаются в глубинах космического пространства и затягиваются в поле гравитации. Существует еще и третья теория неизвестного происхождения, которая рассмотрена и прокомментирована профессором у.-Г. Пикерингом и согласно которой Луна оторвалась от Земли, когда последняя частично уплотнилась. Это привело к образованию континентов, которые, вероятно, не могли сформироваться иным способом.
В последнее время эта признанная теория подвергается критике со стороны профессора т. Дж. Дж. Си в его выдающемся труде «Эволюция звёздных систем», в котором он утверждает, что центробежная сила совершенно недостаточна, чтобы осуществить отделение, и что все планеты, включая Луну, зарождаются в глубинах космического пространства и затягиваются в поле гравитации. Существует еще и третья теория неизвестного происхождения, которая рассмотрена и прокомментирована профессором у.-Г. Пикерингом и согласно которой Луна оторвалась от Земли, когда последняя частично уплотнилась. Это привело к образованию континентов, которые, вероятно, не могли сформироваться иным способом.
Несомненно, планеты и спутники зарождаются и тем, и другим способом, и, по моему мнению, выяснить характер их происхождения нетрудно. Не рискуя ошибиться, можно сделать следующие выводы:
1. Небесное тело, отброшенное от более крупного, не может вращаться на собственной оси. Масса, превратившаяся в жидкость под комплексным воздействием теплоты и давления, после снижения последнего немедленно застывает, одновременно подвергаясь деформации, вызванной гравитационным притяжением. Образовавшаяся форма обретает постоянные очертания после охлаждения и отвердевания, и меньшая масса продолжает двигаться вокруг большей, как если бы она была жестко соединена с ней, если не считать маятниковых колебаний, или вибраций, вследствие изменения орбитальной скорости. такое движение исключает возможность осевого вращения в строго физическом смысле. Луна никогда не вращалась, и это наглядно демонстрирует тот факт, что точнейшими измерениями не удается доказать хоть какое-то сплющивание шара.
Образовавшаяся форма обретает постоянные очертания после охлаждения и отвердевания, и меньшая масса продолжает двигаться вокруг большей, как если бы она была жестко соединена с ней, если не считать маятниковых колебаний, или вибраций, вследствие изменения орбитальной скорости. такое движение исключает возможность осевого вращения в строго физическом смысле. Луна никогда не вращалась, и это наглядно демонстрирует тот факт, что точнейшими измерениями не удается доказать хоть какое-то сплющивание шара.
2. Если планетарное тело, двигаясь орбитально, обращено одной и той же стороной к основному телу, это со всей определенностью доказывает, что оно отделилось от последнего и является подлинным спутником.
3. Планета, вращающаяся на своей оси, совершая движение вокруг другой планеты, не может быть отброшена от вышеупомянутой, но должна образоваться под воздействием сил гравитации.
Орбита Луны — frwiki.wiki
Эта статья об орбите Луны вокруг Земли. Для орбиты объекта вокруг Луны см. Лунную орбиту .
Лунную орбиту .
Схема системы Земля — Луна. Шкала расстояний не соблюдается.
В данной статье рассматриваются с орбиты на Луну вокруг Земли .
Луна делает один орбиту вокруг Земли примерно за 27,32 дней до 384400 км от центра Земли в среднем, при средней скорости 683,590 3 215 км / ч . Он отличается от большинства естественных спутников других планет тем, что его орбита ближе к плоскости эклиптики, чем к экватору Земли .
Хотя в целом орбита Луны имеет форму эллипса, она демонстрирует множество нарушений (известных как возмущения ), изучение которых имеет очень долгую историю.
Резюме
- 1 Недвижимость
- 1.1 Эксцентриситет
- 1.1.1 Вариация в размере 29,53 дня
- 1.1.2 Вариация в темпе 205,9 дней
- 1.2 Прецессия перигея
- 1.
 3 Узлы
3 Узлы - 1.4 Наклон
- 1.5 Прецессия оси вращения
- 1.6 Лунистице
- 1.7 Двойная планета
- 1.8 Орбитальные элементы
- 1.1 Эксцентриситет
- 2 лунных периода
- 3 прилива
- 4 Релиз
- 4.1 Продольный выпуск
- 4.2 Продольный выпуск
- 4.3 Дневной выпуск
- 5 Траектория
- 6 Примечания и ссылки
- 7 Библиография
- 8 Приложения
- 8.1 Внутренние ссылки
Характеристики
Эксцентриситет
Орбита Луны явно эллиптическая , со средним эксцентриситетом 0,054 9. Эта некруглая форма вызывает изменение угловой скорости и видимого размера Луны для наблюдателя с Земли. Среднесуточное угловое движение Луны для воображаемого наблюдателя , находящегося на барицентре два небесных объектов 13,176 ° восточной долготы.
Однако эксцентриситет Луны далеко не постоянен во времени. Действительно, из-за солнечных возмущений этот эксцентриситет варьируется от 0,0255 до 0,0775. Два основных варианта имеют период 29,53 дня и 205,9 дня.
Два основных варианта имеют период 29,53 дня и 205,9 дня.
Вариация в размере 29,53 суток
Изменение в 29,53 дня напрямую связано с положением Луны на ее орбите относительно Солнца, отсюда и тот факт, что период совпадает с синодическим периодом Луны.
Вариация в темпе 205,9 дней
Вариация со скоростью 205,9 суток связана с ориентацией самой лунной орбиты. Действительно, эксцентриситет достигает максимума, когда большая ось орбиты Луны совмещена с осью Земля-Солнце. И наоборот, эксцентриситет минимален, когда большая ось орбиты Луны расположена на 90 ° от оси Земля-Солнце. Период этой вариации чуть больше полугода (182,6 суток) из-за прецессии перигея.
Прецессия перигея
Ориентация орбиты нестабильна в пространстве, но со временем претерпевает эффект прецессии . Линия апсид , соединяющая перигей (ближайшую к Земле точку орбиты) и апогей (наиболее удаленную точку), медленно вращается в том же направлении, что и сама Луна (прямое движение). Эта прецессия лунного перигея совершает полный оборот за 3232,605 4 дня (примерно 8,85 года).
Узлы
В узлах являются точками орбиты , которая пересекает плоскость эклиптики . Луна пересекает восходящий узел каждые 27 212 2 дня, что является драконовским месяцем . Линия узлов, пересечение между орбитальной плоскостью Луны и плоскостью эклиптики, претерпевает ретроградное движение : для земного наблюдателя она поворачивается на запад, совершая полный оборот за 18,60 лет, то есть 19,354 9 ° за год. С точки зрения воображаемого наблюдателя, находящегося на северном полюсе мира , узлы вращаются вокруг Земли в отрицательном направлении, противоположном его собственному вращению и его вращению вокруг Солнца.
Затмения Солнца и Луны происходят только тогда, когда узлы выровнены (или наиболее близки) к оси Солнце-Земля, этот период выравнивания, благоприятный для затмений, называется сезоном затмений , он происходит примерно каждые 173,3 дня.
Наклон
Наклон орбиты Луны на плоскости эклиптики имеет 5. 145 ° в среднем и варьируется от 5 до 5,28 ° в соответствии с циклом 173 дней (половины года draconite ). Луны «с осью вращения не перпендикулярна плоскости его орбиты и лунным экватор наклонен 1.543 ° по эклиптике.
145 ° в среднем и варьируется от 5 до 5,28 ° в соответствии с циклом 173 дней (половины года draconite ). Луны «с осью вращения не перпендикулярна плоскости его орбиты и лунным экватор наклонен 1.543 ° по эклиптике.
Ось вращения Луны и ее плоскость орбиты испытывают идентичный эффект прецессии: таким образом, хотя ее ось вращения не фиксирована относительно звезд, угол между плоскостью лунного экватора и эклиптикой всегда равен 1,543. ° .
Прецессия оси вращения
Ось вращения Луны претерпевает прецессию с периодом 6793,5 суток (18,599 6 лет). Эта прецессия вызвана гравитацией Солнца и, в меньшей степени, экваториальным краем Земли.
Поскольку сама Земля наклонена на 23,45 градуса относительно эклиптики, наклон плоскости лунной орбиты относительно экватора Земли варьируется от 28,72 градуса до 18,16 градуса.
Lunistice
Во время июньского солнцестояния эклиптика достигает максимального склонения в южном полушарии — -23 ° 29 ′. В то же время, когда восходящий узел Луны образует прямой угол с Солнцем, склонение полной Луны достигает минимум -28 ° 36 ′. Этот эффект называется южной лунистостью .
Девять с половиной лет спустя, когда нисходящий узел Луны образует прямой угол с Солнцем во время декабрьского солнцестояния, склонение Луны достигает максимума 28 ° 36 ‘, северного лунного сияния.
Двойная планета
Масштабный вид Земли и Луны.
Масса Земли составляет 81 раз больше , чем Луны, коэффициент значительно ниже , чем у большинства спутников в Солнечной системе; однако барицентры двух тел по-прежнему находятся внутри Земли, примерно на 1750 км ниже ее поверхности. Кроме того, Луна не вращается по орбите в плоскости экватора Земли, опять же, в отличие от большинства спутников. По этим причинам, среди прочего, пара Земля-Луна иногда рассматривается как двойная планета, а не система планета-спутник .
По этим причинам, среди прочего, пара Земля-Луна иногда рассматривается как двойная планета, а не система планета-спутник .
Орбитальные элементы
Следующие параметры суммируют основные характеристики орбиты Луны:
- Большая полуось : 384748 км
- Расстояние до перигея : ~ 362 600 км (от 356 400 до 370 400 км )
- Расстояние на пике : ~ 405 400 км (от 404 000 до 406 700 км )
- Среднее значение эксцентриситета : 900 6 0,054 (от 0,026 до 0,077)
- Среднее наклонение орбиты на эклиптике: 5,14 ° (от 4,99 до 5,30 °)
- Средний наклон : 6,68 °
- Средний наклон лунного экватора к эклиптике: 1,543 °
- Период прецессии узла: 18,599 6 лет
- Период прецессии линии апсид: 8 850 4 года
Лунные периоды
Для описания времени, необходимого для оборота Луны вокруг Земли, можно использовать несколько методов. Сидерический месяц это период обращения Луны относительно неподвижных звезд, и около 27,3 дней. Синодический месяц это период между двумя одинаковыми фазами Луны , около 29,5 дней. Синодический месяц длиннее сидерического месяца, потому что система Земля-Луна движется по своей орбите вокруг Солнца, и поэтому требуется немного больше времени для достижения той же конфигурации.
Сидерический месяц это период обращения Луны относительно неподвижных звезд, и около 27,3 дней. Синодический месяц это период между двумя одинаковыми фазами Луны , около 29,5 дней. Синодический месяц длиннее сидерического месяца, потому что система Земля-Луна движется по своей орбите вокруг Солнца, и поэтому требуется немного больше времени для достижения той же конфигурации.
Аномалистический месяц это период между два перигеем , тем draconit месяц между двумя восходящими узлами и тропическим месяцем между двумя проходами в той же эклиптике долготы . Из-за прецессии лунной орбиты эти периоды не имеют такой же продолжительности, как сидерический месяц.
| Фамилия | Стоимость (дни) | Определение |
|---|---|---|
| Сидерический период | 27 321 661 | По сравнению с далекими звездами |
| Синодический период | 29 530 588 | Относительно Солнца (фазы Луны или луны ) |
| Тропический период | 27 321 582 | Относительно весенней точки (прецессия ~ 26000 а ) |
| Аномалистический период | 27,554 550 | Относительно перигея (прецессия за 3232,6 суток = 8,8504 а) |
| Драконитический период | 27 212 220 | Относительно восходящего узла (прецессия за 6793,5 дня = 18,5996 а) |
В итоге :
- Драконитовый месяц: 27 212 220 815 дней
- Тропический месяц: 27 321 582 дня
- Сидерический месяц: 27,321,661 55 дней
- Аномалистический месяц: 27,554,550 дней
- Синодический месяц: 29 530 588 86 дней
- Средний календарный месяц (одна двенадцатая земного года): 30 436 875 дней (по григорианскому календарю) или 30 436 849 9 дней (астрономические)
Приливы
Из-за приливных сил при деформации Земли вдоль оси Земля-Луна часть ее углового момента постепенно передается орбитальному моменту пары Земля-Луна. В результате Луна удаляется от Земли примерно на 38 мм в год. Сохранение углового момента приводит к замедлению вращения Земли, при этом земные сутки удлиняются примерно на 23 мкс в год.
В результате Луна удаляется от Земли примерно на 38 мм в год. Сохранение углового момента приводит к замедлению вращения Земли, при этом земные сутки удлиняются примерно на 23 мкс в год.
В прошлом эти значения были ниже: 620 миллионов лет назад Луна удалялась примерно на 22 мм в год, а земные сутки удлинялись на 12 мкс в год.
Текущие расчеты предполагают, что Луна продолжит удаляться от Земли еще 50 миллиардов лет. В это время Земля и Луна должны находиться в синхронном вращении : Луна должна вращаться вокруг Земли за 47 дней, и два тела должны вращаться вокруг себя одновременно, всегда противостоящие одному лицу (что уже имеет место в Луна). Такая ситуация уже достигнута для Плутона и его спутника Харона с периодом 6,375 дня.
Такая ситуация уже достигнута для Плутона и его спутника Харона с периодом 6,375 дня.
Однако эти расчеты не принимают во внимание эволюцию Солнца в течение этого периода, а также эффекты преобразований атмосферы и океанов Земли, которые будут иметь место в период с настоящего момента.
Релиз
Продольный выпуск
Моделирование Луны во время полной луны. Освобождение — это кажущееся колебание Луны в этот период.
Луна находится в синхронном вращении и поэтому всегда обращена одним и тем же лицом к Земле. Однако это синхронное вращение верно только в среднем из-за его орбитального эксцентриситета . Следовательно, угловая скорость Луны меняется во время одного обращения и не всегда равна ее скорости вращения. Когда Луна находится в перигее , ее вращение медленнее, чем ее орбитальное движение, что позволяет видеть до 8 ° долготы восточной части ее обратной стороны . Наоборот, в апогее вращение быстрее, обнаруживая 8 ° долготы его западной части. Этот эффект известен как продольная либрация .
Этот эффект известен как продольная либрация .
Широтный выпуск
Поскольку ось вращения Луны наклонена на 1,5 ° в плоскости орбиты, а сама она наклонена на 5,2 ° по эклиптике, видимая часть для земного наблюдателя может на 6,7 ° превышать Северный полюс или Юг во время обращения. Этот эффект известен как широтная либрация.
Дневной выпуск
Поскольку Луна расположена примерно в 60 земных радиусах от барицентра системы Земля-Луна, наблюдатель на экваторе Земли воспринимает дополнительный 1 ° лунной долготы между восходом и заходом спутника, эффект, известный как дневная либрация. По той же причине наблюдатели на полюсах воспринимают дополнительный 1 ° широты.
Наклон Земли изменяется на 0,002 56 градусов по обе стороны от среднего значения, так называемая нутация , впервые отмеченная Джеймсом Брэдли в 1748 году (см. Также Либрации по широте ).
Также Либрации по широте ).
Дорожка
Схема части пути Земли и Луны вокруг Солнца (внизу, вне схемы): путь Луны всегда выпуклый.
Если смотреть с северного полюса мира , Луна вращается вокруг Земли против часовой стрелки , Земля вращается вокруг Солнца также против часовой стрелки, а Луна и Земля вращаются вокруг своих осей также против часовой стрелки.
В отличие от многих других спутников Солнечной системы, траектория Луны очень похожа на траекторию планеты, вокруг которой она вращается. В гелиоцентрической системе отсчета , то ускорение Луны всегда направлена в сторону Солнца; следовательно, его траектория выглядит выпуклой , никогда не вогнутой и не загибающейся.
Примечания и ссылки
- Эта статья частично или полностью взята из статьи « Луна » (см. Список авторов ) .
- ↑ (в) « Луна Земли: факты и цифры » , Solar System Exploration , НАСА (доступ 9 декабря 2011 г.
 ) .
) . - ↑ (in) Мартин К. Гуцвиллер , « Луна-Земля-Солнце: старейшая проблема трех тел » , Reviews of Modern Physics , Vol. 70, п о 2, стр. 589–639 ( DOI 10.1103 / RevModPhys.70.589 , Bibcode 1998RvMP … 70..589G ).
- ↑ Еспенак .
- ↑ Larousse editions , « Larousse encyclopedia online — latin moon luna » , на www.larousse.fr (по состоянию на 14 декабря 2019 г. )
- ↑ (in) Г-н Шапрон-Тузе Шапрон Ж.
 , » Лунные эфемериды ELP-2000 » , Astronomy & Astrophysics , vol. 124,, стр. 54 ( Bibcode 1983A & A … 124 … 50C ).
, » Лунные эфемериды ELP-2000 » , Astronomy & Astrophysics , vol. 124,, стр. 54 ( Bibcode 1983A & A … 124 … 50C ). - ↑ (405 400/362 600 — 1) / 2 = 0,005 90
- ↑ a и b Жан Миус, Кусочки математической астрономии (Ричмонд, Вирджиния: Willmann-Bell, 1997) 11–12.
- ↑ (in) CD Мюррей и С.Ф. Дермотт, Динамика солнечной системы , Cambridge University Press ,, стр. 184.
- ↑ (in) Теренс Дикинсон , От Большого взрыва до Планеты X , Кэмден-Ист, Онтарио, Камден Хаус ,, 151 с. ( ISBN 0-921820-71-2 ) , стр. 79–81.
- ↑ a и b (in) Хельмер Аслаксен , « Орбита Луны вокруг Солнца выпуклая! » ,(по состоянию на 21 апреля 2006 г. ) .
- ↑ Луна всегда поворачивается к Солнцу на MathPages .
- ↑ (in) HL Vacher , « Computational Geology 18 — Definition and the Concept of Set » , Journal of Geoscience Education , vol. 49, п о 5,, стр. 470–479 ( читать онлайн [PDF] , по состоянию на 21 апреля 2006 г. ).
Библиография
: документ, использованный в качестве источника для этой статьи.
- [Эспенак] Фред Эспенак, GSFC НАСА, » Затмения и орбита Луны «, веб-сайт NASA Eclipse , (дата неизвестна) ( читать онлайн ).
Приложения
Внутренние ссылки
- Луна
- Орбита
- Сарос (223 лунных месяца )
- Inex (358 лунок )
луна | ||
|---|---|---|
| Орбита |
| |
| Селенография |
| |
| Списки |
| |
| Физика Луны |
| |
| Исследование |
| |
| Календарь |
| |
| Мифы и искусства | Мифы :
Комикс :
Кино :
| |
<img src=»//fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Луна вращается? | Космос
Полный оборот Луна совершает чуть более чем за 27 дней. (Изображение предоставлено: NASA/Студия научной визуализации Центра космических полетов имени Годдарда)Наблюдатели на Земле могут заметить, что Луна, по существу, держится той же стороной, обращенной к нашей планете, когда проходит по своей орбите. Это может привести к вопросу, вращается ли Луна? Ответ положительный, хотя это может показаться противоречащим тому, что видят наши глаза.
Ближняя и дальняя стороны Луны
Луна делает один оборот вокруг Земли за 27,322 дня. Луне также требуется примерно 27 дней, чтобы совершить один оборот вокруг своей оси. В результате кажется, что Луна не вращается, но наблюдателям с Земли кажется, что она почти совершенно неподвижна. Ученые называют это синхронным вращением.
Сторона Луны, постоянно обращенная к Земле, известна как ближняя сторона. Противоположная или «обратная» сторона — это дальняя сторона. Иногда обратную сторону Луны называют темной стороной, но это неверно. Когда Луна находится между Землей и Солнцем, во время одной из лунных фаз, называемой новолунием, обратная сторона Луны залита дневным светом.
Иногда обратную сторону Луны называют темной стороной, но это неверно. Когда Луна находится между Землей и Солнцем, во время одной из лунных фаз, называемой новолунием, обратная сторона Луны залита дневным светом.
Однако орбита и вращение не совсем совпадают. Луна движется вокруг Земли по эллиптической орбите, слегка вытянутой окружности. Когда Луна находится ближе всего к Земле, ее вращение медленнее, чем ее путешествие в космосе, что позволяет наблюдателям видеть дополнительные 8 градусов на восточной стороне. Когда Луна находится дальше всего, вращение происходит быстрее, поэтому с западной стороны видны дополнительные 8 градусов.
Связанный: Луна: 10 удивительных фактов о Луне
Если бы вы могли отправиться на обратную сторону Луны, как это когда-то сделали астронавты Аполлона-8, вы бы увидели совсем другую поверхность, чем та, которую вы привыкли видеть. В то время как ближняя сторона Луны сглажена морями — большими темными равнинами, созданными затвердевшими потоками лавы — и светлыми лунными нагорьями, обратная сторона покрыта кратерами.
Хотя ты не можешь увидеть обратную сторону Луны с Земли, НАСА и другие космические агентства видели ее со спутников.
«Удивительно, насколько Земля ярче Луны», — сказал Адам Сабо, ученый проекта спутника NASA Deep Space Climate Observatory в Центре космических полетов имени Годдарда в Гринбелте, штат Мэриленд, после того, как спутник заснял луну, пересекающую поверхность Земли. . «Наша планета — поистине блестящий объект в темном космосе по сравнению с лунной поверхностью».
Изменение орбиты Луны
Период вращения Луны не всегда был равен ее орбите вокруг планеты. Точно так же, как гравитация Луны влияет на океанские приливы на Земле, гравитация Земли влияет на Луну. Но поскольку на Луне нет океана, Земля тянет свою кору, создавая приливную выпуклость на линии, указывающей на Землю.
Инфографика : Внутри земной луны
Гравитация Земли притягивает ближайшую приливную выпуклость, пытаясь удержать ее на одном уровне. Это создает приливное трение, которое замедляет вращение Луны. Со временем вращение замедлилось настолько, что орбита и вращение Луны совпали, и одно и то же лицо стало заблокированным приливом, навсегда направленным к Земле.
Со временем вращение замедлилось настолько, что орбита и вращение Луны совпали, и одно и то же лицо стало заблокированным приливом, навсегда направленным к Земле.
Луна — не единственный спутник, испытывающий трение со своей родительской планетой. Многие другие крупные спутники Солнечной системы связаны приливами со своим партнером. Из более крупных спутников только спутник Сатурна Гиперион, который хаотично кувыркается и взаимодействует с другими спутниками, не синхронизирован с приливами.
Вращение Луны определило, был ли печально известный Человек на Луне, похожий на лицо образец темных морей на стороне, обращенной к Земле, направлен на нашу планету. Гравитация создала выпуклость на стороне Земли на Луне, замедлив ее вращение в прошлом, чтобы создать синхронное вращение и удерживая более длинную лунную ось в направлении нашего мира.
Недавние исследования показали, что сторона Луны, обращенная к Земле, определяется тем, насколько быстро замедляется лунное вращение. Поскольку Луна медленно теряла скорость, вероятность того, что Человек на Луне окажется лицом к Земле, а не из космоса, была примерно два к одному.
Поскольку Луна медленно теряла скорость, вероятность того, что Человек на Луне окажется лицом к Земле, а не из космоса, была примерно два к одному.
«Настоящее совпадение заключается не в том, что человек смотрит на Землю», — говорится в заявлении Одеда Ааронсона, исследователя планетологии из Калифорнийского технологического института, изучавшего, почему человек на Луне смотрит на Землю. Вместо этого, настоящее совпадение заключается в том, что замедления Луны было достаточно, чтобы загрузить монету.
Ситуация не ограничивается большими планетами. Карликовая планета Плутон приливно привязана к своему спутнику Харону, который почти такой же большой, как предыдущая планета.
Земля (и другие планеты) не остаются полностью невредимыми. Точно так же, как Земля оказывает трение на вращение Луны, Луна также оказывает трение на вращение Земли. Таким образом, продолжительность дня увеличивается на несколько миллисекунд каждое столетие.
«Луна и Земля вырисовывались большими в небе друг друга, когда они сформировались», — сказала в своем заявлении тогдашняя аспирантка Арпита Рой.
«Во времена динозавров Земля совершала один оборот примерно за 23 часа», — говорится в заявлении Дэниела Макмиллана из Центра космических полетов имени Годдарда НАСА в Гринбелте, штат Мэриленд. «В 1820 году оборот занял ровно 24 часа, или 86 400 стандартных секунд. С 1820 года средний солнечный день увеличился примерно на 2,5 миллисекунды».
30 июня 2012 года из-за этого явления ко всем часам на Земле добавилась дополнительная секунда.
Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: [email protected].
Нола Тейлор Тиллман — автор статей для Space.com. Она любит все, что связано с космосом и астрономией, и наслаждается возможностью узнать больше. Она имеет степень бакалавра английского языка и астрофизики в колледже Агнес Скотт и проходила стажировку в журнале Sky & Telescope. В свободное время она обучает своих четверых детей дома. Подпишитесь на нее в Твиттере @NolaTRedd
Подпишитесь на нее в Твиттере @NolaTRedd
лучших вопросов о Луне | Внутри и снаружи — Луна: NASA Science
Ответы на некоторые из ваших часто задаваемых вопросов о Луне.
Луна в движении: фазы, закономерности и многое другое
Луна вращается? Луна вращается вокруг своей оси?
Да! Время, за которое Луна совершает оборотов вокруг своей оси на оборотов, равно времени, которое требуется Луне для совершения оборотов вокруг Земли на оборотов. Это удерживает одну и ту же сторону Луны, обращенную к Земле в течение месяца.
Если бы Луна вообще не вращалась вокруг своей оси, или если бы она вращалась с любой другой скоростью, то в течение месяца мы бы видели разные части Луны.
Луна вращается вокруг Земли?
Да. Луне требуется около одного месяца, чтобы совершить оборот вокруг Земли (27,3 дня, чтобы совершить оборот, но 29,5 дня, чтобы перейти от новолуния к новолунию).
Поскольку Луна совершает каждый 27,3-дневный оборот вокруг Земли, и Земля, и Луна движутся вокруг Солнца.
 Из-за этого изменения положения солнечный свет падает на Луну под немного другим углом в 27-й день, чем в нулевой день, хотя сама Луна уже прошла весь путь вокруг Земли. Солнечному свету требуется чуть больше двух дополнительных дней, чтобы попасть на Луну так же, как это произошло в нулевой день. Вот почему требуется 290,5 дней, чтобы добраться от новолуния до новолуния, хотя самой Луне требуется не так много времени, чтобы совершить один оборот вокруг Земли.
Из-за этого изменения положения солнечный свет падает на Луну под немного другим углом в 27-й день, чем в нулевой день, хотя сама Луна уже прошла весь путь вокруг Земли. Солнечному свету требуется чуть больше двух дополнительных дней, чтобы попасть на Луну так же, как это произошло в нулевой день. Вот почему требуется 290,5 дней, чтобы добраться от новолуния до новолуния, хотя самой Луне требуется не так много времени, чтобы совершить один оборот вокруг Земли.Фазы Луны одинаковы везде на Земле?
Да, все видят одни и те же фазы Луны. Однако люди к северу и югу от экватора видят текущую фазу Луны под разными углами. Если бы вы путешествовали в другое полушарие, Луна была бы в той же фазе, что и дома, но казалась бы перевернутой по сравнению с тем, к чему вы привыкли!
Например, 8 марта 2021 года Луна находилась в фазе убывающей серпы. Если смотреть из северного полушария, на левой стороне Луны появился убывающий полумесяц. При взгляде из Южного полушария полумесяц оказался справа.
Визуализация данных убывающего полумесяца из Северного полушария (слева) и Южного полушария (справа) 8 марта 2021 года. Предоставлено: Студия научной визуализации НАСА.
Фазы Луны вызваны тенями от Земли?
Нет. Тень Земли влияет на наш взгляд на Луну только во время лунных затмений. Как правило, одна половина Луны — сторона, обращенная к Солнцу, — ярко освещена, а другая находится в тени. Мы используем фазы луны , чтобы описать, как меняется наша точка зрения на полуосвещенную Луну по мере того, как Земля и Луна перемещаются в космосе в течение месяца.
Во время полумесяца, например, часть Луны, обращенная к Земле, в основном находится в тени, а обратная сторона Луны в основном освещена солнцем. Видимый полумесяц — единственная часть ближней стороны Луны, на которой наблюдается дневное время.
Визуализация данных убывающего полумесяца, видимого из северного полушария. Во время этой фазы на большей части ближней стороны Луны ночь, а на большей части дальней стороны Луны день. Авторы и права: Студия научной визуализации НАСА.
Авторы и права: Студия научной визуализации НАСА.Почему мы видим фазы Луны?
Луна всегда наполовину освещена солнцем (кроме лунного затмения). Сторона Луны, обращенная к Солнцу, кажется яркой из-за отраженного солнечного света, а сторона Луны, обращенная от Солнца, темная. Наш взгляд на полуосвещенную Луну меняется по мере того, как Луна вращается вокруг Земли. Когда ближайшая к нам сторона полностью освещена, мы называем это полной Луной. Когда дальняя сторона полностью освещена, а ближняя темна, мы называем это новолунием. Когда мы видим другие фазы, мы смотрим на разделение между лунной ночью (темная часть) и днем (яркая часть).
Какова на самом деле форма Луны?
Луна имеет форму несовершенной сферы. Издалека он кажется почти круглым. Если смотреть вблизи, поверхность Луны представляет собой трехмерный пейзаж с горами, долинами и кратерами. Исследуйте поверхность Луны, где бы вы ни находились, на этой 3D-карте, созданной на основе данных, полученных Лунным разведывательным орбитальным аппаратом НАСА (LRO).

Можно ли увидеть Луну днем?
Да! Луна днем так же высоко, как и ночью, но вы можете не так легко это заметить. Поскольку Солнце также восходит, а фазы Луны , которые чаще всего видны при дневном свете, показывают нам лишь небольшую часть яркой стороны Луны (например, фазы полумесяца), Луну труднее увидеть днем.
Почему Луна восходит и заходит? Могут ли жители разных стран увидеть Луну в один и тот же день?
Восходы и заходы луны происходят по той же причине, что и восходы и закаты. Земля вращается каждый день! Это означает, что наблюдатели во многих разных частях мира по очереди смотрят на Луну в течение дня, точно так же, как все мы видим одно и то же Солнце в течение 24 часов.
Почему Луна кажется самой большой вблизи горизонта?
Это оптическая иллюзия. Докажите это сами здесь!
Происхождение и природа Луны
Луна излучает свой собственный свет (как Солнце)?
Луна не излучает собственный свет.
 «Лунный свет» — это на самом деле солнечный свет, отражающийся от поверхности Луны.
«Лунный свет» — это на самом деле солнечный свет, отражающийся от поверхности Луны.Что такое лунный свет? Как освещается Луна?
Луна не излучает собственный свет. Весь лунный свет — это отраженный солнечный свет. Яркая часть Луны переживает дневное время.
Что такое Луна? Это планета?
Луна — это естественный спутник или космический объект, вращающийся вокруг чего-то другого. Наша Луна — естественный спутник Земли.
В общем, луна — это естественный спутник планеты, а планета — это особый вид естественного спутника, который вращается вокруг звезды, а также удовлетворяет другим условиям.
Подробнее: Что делает планету планетой?
Как образовалась Луна?
Основная теория состоит в том, что объект размером с Марс столкнулся с Землей миллиарды лет назад, и обломки этого столкновения в конечном итоге сформировали Луну. Вот анимация, показывающая, как это могло бы выглядеть:
youtube.com/embed/UIKmSQqp8wY» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Для получения дополнительной информации посетите веб-страницу The Moon In Depth.
Есть ли на Луне гравитация? Вещи всплывают «вверх», когда их роняют на Луну?
На Луне есть гравитация. Поскольку Луна имеет меньшую массу, чем Земля, ее гравитационное притяжение слабее (примерно в шесть раз меньше земного). На Луне вы сможете прыгнуть примерно в шесть раз выше, чем на Земле, — но вы все равно вернетесь вниз!
Что было бы, если бы не было Луны? Как Луна влияет на Землю?
Земля была бы совсем другим миром, если бы на ней не было Луны. Гравитация Луны не дает нашей планете слишком сильно колебаться вокруг своей оси, что помогает стабилизировать наш климат. Луна также играет важную роль в создании приливов в океанах Земли.
Луна в движении: фазы, закономерности и многое другое
Происхождение и природа Луны
Журнал наблюдений за Луной
Карты Луны 2022 года для International Observe the Moon Night
Лунная тайна: Купола Груйтуйзен
Вам также может понравиться
Луна вращается? | Живая наука
Различные фазы Луны, как видно с Земли. (Изображение предоставлено: Яорушэн через Getty Images)
(Изображение предоставлено: Яорушэн через Getty Images)Каждые 24 часа поверхность Земли купается во тьме и солнечном свете, так как планета завершает один день. Восход и закат происходят как по маслу, поскольку Земля постоянно вращается вокруг своей оси. А как насчет спутника Земли, луна — тоже вращается?
Ответ: да, Луна вращается, но гораздо медленнее, чем Земля. По данным НАСА, «лунный день» составляет около 29,53 земных дня. Другими словами, в то время как Земля совершает один оборот за 24 часа, Луна восходит примерно каждые 709 часов.
Как и у многих небесных тел, вращательное движение Луны может быть остатком от ее создания. Одна из теорий, называемая гипотезой гигантского удара, предполагает, что около 4,5 миллиардов лет назад тело размером примерно с Марс врезалось во все еще развивающуюся Землю.0203 согласно НАСА . Этот теоретический объект известен как Тейя, и тепло от удара Тейи, возможно, создало океаны магмы, расплавив земную кору, и заставило Землю выбросить вращающиеся испаренные частицы в космос.
Связанный: Сколько времени потребуется, чтобы обойти Луну?
Согласно гипотезе гигантского столкновения, эти облака пыли и газа вращались от силы первоначального столкновения. В конце концов, эти закрученные частицы соединились, потому что масса притягивает массу, и когда газ сконденсировался, она на самом деле стал быстрее крутиться . Представьте себе фигуриста, который сгибает руки во время вращения на льду. Масса конькобежца более компактна ближе к их середине, поэтому конькобежец ускоряется. Это связано с тем, что их угловой момент сохраняется — произведение силы вращения, необходимой для вращения объекта, или момента инерции, и угловой скорости. Другими словами, требуется больше силы, чтобы повернуть объект дальше от центра тяжести. Так, если руки фигуриста вытянуты, они вращаются медленнее, а когда они меняются, сводя их, они вращаются быстрее.
Луна сохранила свой угловой момент с момента первоначального столкновения миллиарды лет назад. «Два вращающихся тела столкнулись друг с другом, и законы физики говорят нам, что образовавшееся массивное пылевое облако продолжит вращаться. В конце концов, это вращающееся пылевое облако сконденсировалось, чтобы сформировать вращающуюся луну», — сказал Даниэль Мориарти, лунный геолог из NASA Goddard. Центр космических полетов и Мэрилендский университет.
«Два вращающихся тела столкнулись друг с другом, и законы физики говорят нам, что образовавшееся массивное пылевое облако продолжит вращаться. В конце концов, это вращающееся пылевое облако сконденсировалось, чтобы сформировать вращающуюся луну», — сказал Даниэль Мориарти, лунный геолог из NASA Goddard. Центр космических полетов и Мэрилендский университет.
В отличие от Земли, на Луне нет атмосферы, поэтому отсутствует сопротивление воздуха, замедляющее движущиеся объекты; как таковые, когда объекты вращаются, они, как правило, продолжают вращаться. Конечно, есть и другие теории о том, как Земля получила свой спутник. Одной из них является теория захвата, согласно которой Луна была блуждающим телом, подобным астероиду, который был захвачен земным гравитационная тяга. Согласно этой теории, Луна была создана где-то еще в Солнечной системе, а затем начала вращаться вокруг Земли, когда она проходила мимо, согласно НАСА , поэтому у нее уже должно было быть собственное вращение, когда она была втянута в гравитационное поле Земли.
Другая теория — это теория совместного образования, согласно которой Луна была создана в то же время, что и Земля. В этой гипотезе два массивных объекта в пять раз больше Марса врезались друг в друга. Затем Земля и ее Луна сконденсировались из облаков материи, возникших в результате столкновения, НАСА сообщило .
Однако именно Земля задает скорость вращения Луны. Луна совершает один оборот примерно за 27 дней — 90 203 почти столько же, сколько 90 204 требуется Луне для обращения вокруг Земли: 27,32 дня. В результате люди на Земле всегда видят только одну сторону Луны. Если бы лунный день был длиннее или короче, мы могли бы видеть всю поверхность Луны, когда Луна вращается вокруг Земли.
Связанный: Почему у луны есть фазы?
На самом деле, орбита и вращение не полностью совпадают, потому что Земля на самом деле движется по овальной эллиптической орбите. Когда Луна находится в точке своей орбиты, ближайшей к Земле, ее вращение медленнее, чем ее орбита, что позволяет нам видеть дополнительные 8 градусов ее поверхности, что мы обычно видим, согласно Space.com, дочернему сайту LiveScience.
Когда Луна находится в точке своей орбиты, ближайшей к Земле, ее вращение медленнее, чем ее орбита, что позволяет нам видеть дополнительные 8 градусов ее поверхности, что мы обычно видим, согласно Space.com, дочернему сайту LiveScience.
Иллюзия того, что луна не вращается с нашей точки зрения, вызвана приливным запиранием или синхронным вращением, при котором заблокированному телу требуется столько же времени, чтобы совершить оборот вокруг своего партнера, сколько ему требуется, чтобы один раз повернуться вокруг своей оси из-за его гравитация партнера. (Луны других планет испытывают тот же эффект.) Кроме того, луна не является идеальным кругом; это криво. «Луна не симметрична», — сказал Мориарти в интервью Live Science. «Существуют различия в массе и плотности между полушариями [луны, обращенной к Земле и от Земли]. Разница настолько велика, что одна сторона Луны [ее более длинная сторона] остается «застрявшей» лицом к Земле из-за гравитации».
СВЯЗАННЫЕ ЗАГАДКИ
«Таким образом, когда Луна вращается вокруг Земли, она поворачивается так, что обращена к нам одной и той же стороной», — сказал Мориарти. «Один оборот занимает столько же времени, сколько один оборот, другими словами, около месяца». Иными словами, Земля и Луна оказывают друг на друга гравитационное притяжение, и приложенная гравитационная сила всегда максимальна там, где два тела обращены прямо друг к другу, в результате чего и Земля, и Луна слегка растягиваются, когда они притягиваются друг к другу. направление другого. В результате Луна вытягивается в эллиптическую форму, а ее самая длинная ось вытягивается, чтобы всегда быть обращенной к нам. Это также то, что заставляет приливы и отливы Земли каждый день.
«Один оборот занимает столько же времени, сколько один оборот, другими словами, около месяца». Иными словами, Земля и Луна оказывают друг на друга гравитационное притяжение, и приложенная гравитационная сила всегда максимальна там, где два тела обращены прямо друг к другу, в результате чего и Земля, и Луна слегка растягиваются, когда они притягиваются друг к другу. направление другого. В результате Луна вытягивается в эллиптическую форму, а ее самая длинная ось вытягивается, чтобы всегда быть обращенной к нам. Это также то, что заставляет приливы и отливы Земли каждый день.
В действительности, Луна может вращаться очень медленно, но ее вращение является ключом к важным событиям, таким как приливы и отливы на Земле.
Приливная блокировка также влияет на движение планет и лун . Это означает, что дни на Земле и на Луне были намного короче, когда эти тела впервые образовались, потому что и Земля, и Луна вращались с гораздо большей скоростью, чем сейчас. Модель , разработанная исследователями из Гарварда и Института SETI, даже оценивает, что на ранней Земле день был всего 2,5 часа во время ее столкновения с Тейей. Однако из-за гравитационного притяжения, постоянно тянущего самую длинную ось Луны к Земле, дни Земли и Луны со временем удлинялись.
Однако из-за гравитационного притяжения, постоянно тянущего самую длинную ось Луны к Земле, дни Земли и Луны со временем удлинялись.
Первоначально опубликовано на Live Science.
Джеклин Кван — независимый журналист из Соединенного Королевства, который в основном освещает вопросы науки и техники. Она окончила Манчестерский университет со степенью магистра физики и в 2021 году получила диплом NCTJ золотого стандарта в области мультимедийной журналистики. Джеклин писала для Wired UK, Current Affairs и Science for the People.
Движение Солнца-Земли-Луны — НАУКА 8 КЛАССА
Все тела Солнечной системы находятся в постоянном движении.
День и ночь
- Земля вращается вокруг своей оси на оборотов, а также оборотов вокруг Солнца. Полное вращение происходит примерно за 24 часа в сутки. Это движение против часовой стрелки происходит с запада на восток, в результате чего кажется, что Солнце восходит на востоке и заходит на западе.

Год
- В то время как Земля вращается вокруг своей оси, она также вращается вокруг Солнца. Для этого движения/орбиты требуется 365 ¼ дней в году.
- Земля вращается вокруг Солнца по эллиптической орбите.
Вращение против вращения
Лунное движение (Луна)
- Луна вращается вокруг своей оси и вращается вокруг Земли, как Земля вращается вокруг Солнца.
- Луне требуется около 27 земных дней, чтобы вращаться вокруг своей оси, и около 29 ½ земных дней (месяца), чтобы она вращалась вокруг Земли.
- Потому что Луна период (время) вращения вокруг своей оси и период обращения вокруг Земли почти одинаковы, Луна всегда обращена к Земле одной и той же стороной.
- Изменения положения Луны по мере ее обращения вокруг Земли приводят к тому, что большая или меньшая часть солнечного света, отраженного от Луны, становится видимой при наблюдении за Луной с Земли.
 Из-за этого кажется, что Луна меняет форму.
Из-за этого кажется, что Луна меняет форму.
Фазы Луны
- Новолуние — Луна расположена между Солнцем и Землей так, что сторона Луны, которая видна с Земли, не видна. Из-за этого кажется, что на ночном небе нет Луны.
- Полнолуние — освещенная Солнцем часть Луны обращена к Земле, в то время как Земля расположена между Солнцем и Луной. Луна видна на небе.
- Освещенная Солнцем часть Луны, видимая с Земли, кажется либо увеличивающейся (увеличивается), либо уменьшающейся (убывает) по мере того, как Луна вращается вокруг Земли.
- Полумесяц — прибывающая или убывающая; видно менее ½ освещенной Солнцем части Луны.
- Полосатая луна — прибывающая или убывающая; Видно более ½ освещенной Солнцем части Луны.
- Первая/Третья четверть Видна -1/2 освещенной Солнцем части Луны.

- первый квартал следует за растущим полумесяцем.
- третья четверть происходит, когда видна половина Луны.
Можете ли вы правильно назвать каждую фазу луны?
Почему у Луны есть фазы?
Затмения
- Затмения происходят, когда объект в пространстве проходит непосредственно между двумя другими объектами или между объектом и наблюдателем.
- солнечное затмение происходит, когда Луна проходит непосредственно между Солнцем и Землей, блокируя солнечный свет и отбрасывая тень на определенную область на Земле. Это может произойти только во время Новолуния.
- лунное затмение происходит, когда Земля проходит непосредственно между Солнцем и Луной, блокируя солнечный свет, так что тень Земли падает на Луну, отбрасывая тень на Луну.
 Это может произойти только во время полнолуния.
Это может произойти только во время полнолуния. - Затмение происходит не в каждое Новолуние и Полнолуние из-за угла обращения Луны вокруг Земли.
Почему затмения не происходят каждый месяц?…
Угол обращения Луны вокруг Земли наклонен.
Приливы
- Приливы — это повышение и понижение уровня поверхностных вод земного океана, вызванное гравитационным воздействием Солнца и Луны на Землю. Воздействие приливов наиболее заметно вдоль береговой линии океана.
- Когда Луна вращается вокруг Земли, воды Земли, находящиеся ближе всего к Луне, выпячиваются к Луне. Эта выпуклость — прилив . Еще один прилив происходит на противоположной стороне Земли. Отливы происходят в районах между двумя приливами.
- Поскольку Земля вращается вокруг своей оси, любое заданное место будет вращаться в приливной выпуклости и из нее .
 Это приводит к смене приливов и отливов в течение 24 часов.
Это приводит к смене приливов и отливов в течение 24 часов. - Когда Солнце и Луна выровнены так, что Луна находится между Солнцем и Землей (новолуние) или Земля находится между Солнцем и Луной (полнолуние), приливы выше, а отливы ниже. Их называют весенние приливы . Когда Солнце и Луна находятся под прямым углом друг к другу (первая и последняя четверть), наблюдаются более низкие приливы и более высокие отливы. Эти приливы называются приливов.
Что вызывает приливы?
Дополнительное обучение
- Ученые могут изучать верхний слой Солнца во время некоторых солнечных затмений. Луна блокирует самые яркие солнечные лучи. Это облегчает ученым возможность увидеть верхний слой Солнца. Что узнали ученые?
- Если бы у Земли не было атмосферы, Луна была бы полностью черной во время полного затмения.
 Вместо этого Луна может принимать различные цвета от темно-коричневого и красного до ярко-оранжевого и желтого. Точный внешний вид зависит от того, сколько пыли и облаков присутствует в атмосфере Земли. Полное затмение, как правило, бывает очень темным после крупных извержений вулканов, поскольку эти события выбрасывают большое количество вулканического пепла в атмосферу Земли. Исследуйте различные цвета во время затмений и причины, почему.
Вместо этого Луна может принимать различные цвета от темно-коричневого и красного до ярко-оранжевого и желтого. Точный внешний вид зависит от того, сколько пыли и облаков присутствует в атмосфере Земли. Полное затмение, как правило, бывает очень темным после крупных извержений вулканов, поскольку эти события выбрасывают большое количество вулканического пепла в атмосферу Земли. Исследуйте различные цвета во время затмений и причины, почему. - Насколько наклонена орбита Луны вокруг Земли по сравнению с орбитой Земли вокруг Солнца. По этой причине затмения не случаются при каждом новолунии и полнолунии; тени не сходятся.
- Луна, вращающаяся вокруг Земли, влияет на время приливов и отливов. Это приводит к тому, что эти приливы происходят в разное время каждый день. Есть ли закономерность в этом изменении? Если да, то насколько он меняется?
ФОН: |
Орбита и фазы Луны
Орбита и фазы ЛуныОрбита и
Фазы Луны
Введение
«Фаза» относится к тому, что Луна показывает разные количество освещенных полушарий, если смотреть с Земли во время ее орбиту вокруг земли.
«Цикл» относится к повторению этих фаз, а также циклов затмений. Мы будем исследовать их здесь.
Понимание наблюдаемых фаз Луны требует понимания
как свет и тень работают по отношению к солнечному свету и
орбита Луны и Земли вокруг Солнца.
Суеверие: Иногда считается, что когда луна яркая и полная, люди сходят с ума. На самом деле нет никакой статистической научной доказательства, подтверждающие это. Это миф.
Также: обратите внимание, что нет монстров, пожирающих солнце, как вы могли бы говорили, слушали ли вы профессора в 2000 г. до н.э.
Одна вещь об изучении лунных фаз: она начинает обращаться в частности, как то, что мы видим, наблюдается в астрономии имеет очень четкое научное объяснение.
Движение Луны
Во-первых, обратите внимание, что если вы будете смотреть на луну ночь за ночью, вы увидите две ключевые особенности, которые являются фундаментальными подсказками к пониманию его движения:- Он движется на восток на фоне звезд.
- Он показывает одну и ту же сторону к Земле во всех фазах.
Учитывая эти факты, можете ли вы сделать вывод, вращается ли Луна вокруг своей оси? (рис. 3-2)
Другие ключевые моменты:
 За 24 часа она перемещается на 13 градусов.
За 24 часа она перемещается на 13 градусов.
Лунные фазы, Фазовый цикл
Луна не излучает собственный свет, поэтому свет, который мы видим, от него то, что просто отражается от солнца.
Когда луна движется по небу, солнце освещает разное количество его поверхности. Таким образом, фаза луны полностью определяется глядя на положение Земли относительно Солнца. Лучший способ увидеть фазы — изучить рисунок (см. также (рис. 3-3) текста).
Луна, кажется, проходит полный набор фаз, если смотреть с Земля из-за ее движения вокруг Земли, как показано ниже:
| Фазы Луны |
На этом рисунке показаны различные положения Луны на ее орбите.
(движение Луны по своей орбите предполагается против часовой стрелки).
Внешний набор рисунков показывает соответствующую фазу , если смотреть со стороны
Земля и общие названия фаз.
Можно увидеть последовательность фаз:
Новый, Прибывающий полумесяц, Первая четверть, прибывающая горбинка, полная,
убывающая горбинка, 3-я четверть, убывающая серп.
Примечание: использование слова «четверть» здесь не относится к тому, как большая часть луны видна, но фаза в цикле.
Цикл лунных фаз занимает 29,5 суток, это СИНОДИЧЕСКИЙ ПЕРИОД.
Почему это больше, чем ЗИДЕРОВЫЙ ПЕРИОД, который составлял 27,3 дня? очень просто: это потому, что луна возвращается к тому же место на небе один раз в сидериальный период, но солнце также движется по небу. Когда луна возвращается к тому же пятно на небе солнце сдвинулось на 27 градусов. Таким образом, Луна теперь имеет чтобы занять некоторое дополнительное время, чтобы наверстать упущенное. (рис. 3-4). Луне требуется около 2 дней, чтобы наверстать упущенное.
(Хороший способ понять восход и заход луны из
книга — посмотреть на картинку на странице 34 текста)
Представьте, что вы стоите с человеческой фигурой на земном шаре.
Теперь ключевым моментом является то, что горизонт, над которым находится луна
видна, это плоскость, перпендикулярная вашему телу. Время
дня дается «восход, закат, полдень, полночь». Это время дня представляется нам, когда Земля вращается так, что США
проходит через них. Пока Земля вращается, положение Луны
на своей орбите почти не меняется, поэтому можно говорить о восходе и заходе Луны.
Когда вы представляете себе вращение Земли и различные времена суток
Проходя мимо, можно увидеть, как отличается восход и заход луны для разных
фазы Луны.)
Это время дня представляется нам, когда Земля вращается так, что США
проходит через них. Пока Земля вращается, положение Луны
на своей орбите почти не меняется, поэтому можно говорить о восходе и заходе Луны.
Когда вы представляете себе вращение Земли и различные времена суток
Проходя мимо, можно увидеть, как отличается восход и заход луны для разных
фазы Луны.)
Краткая информация о движении и фазах Луны
Кажется, что Луна совершает полный оборот вокруг небесной сферы примерно раз в 27,3 дня по наблюдению с Земли (звездное месяц) и отражает соответствующий орбитальный период в 27,3 дняЛуне требуется 29,5 дня, чтобы вернуться в ту же точку на небесной сфере. со ссылкой на Солнце из-за движение Земли вокруг Солнца (синодическое месяц)
Лунные фазы, наблюдаемые с Земли, коррелируют с синодический месяц.
Поскольку Луна должна двигаться на восток среди созвездий, достаточно, чтобы
полностью обогнуть небо (360 градусов) за 27,3 дня, он должен двигаться на восток
на 13,2 градуса каждый день
(напротив, помните, что Солнце только кажется
двигаться на восток примерно на 1 градус в день).


 4 “
4 “ 199*10 10 км 3
199*10 10 км 3 00000000
00000000 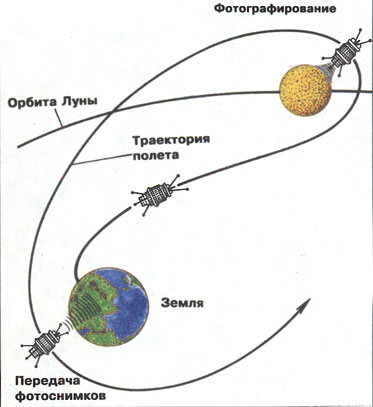 62506250
62506250