МиГ-25рб — Авіамузей

МиГ-25 до сих пор является самым быстрым в мире боевым самолетом, способным летать почти втрое быстрее звука. Его разработку начали в конце 50-х годов, в ответ на разработку американцами нескольких проектов боевых самолетов со скоростями порядка 2.5-3М. Создавалось одновременно два варианта: истребитель-перехватчик Е-155П (для противодействия подобным машинам «вероятного противника») и разведчик-бомбардировщик Е-155Р, «Неуязвимый» для вражеской ПВО благодаря огромной в то время скорости и высоте полета.

При конструировании пришлось преодолевать многие проблемы — например, так называемый «тепловой барьер”: на скоростях свыше М = 2.5 поверхность самолета разогревалась до нескольких сот градусов, и обычный дюралюминий терял прочность. Поэтому основным конструкционным материалом для новой машины стала нержавеющая сталь (80% общей массы планера) и титановые сплавы (8% массы). Из специального жаростойкого дюралюминиевого сплава было выполнено лишь несиловые элементы (11% массы).

Фюзеляж сделали сварным неразъемным. Его центральную часть занимает интегральный топливный бак. В задней части монтируются двигатели, в носовом отсеке — или радар (в истребителя), или аэрофотоаппараты и радиотехническое разведывательное оборудование (у разведчика).

Разведывательный вариант был построен первым, и первым поднялся в воздухе 6 марта 1964 г. После завершения программы государственных испытаний в 1969 году его взяли на вооружение и начали серийно производить на авиазаводе в г. Горький (сейчас Нижний Новгород) под индексом МиГ-25Р («Изделие 02»).

В 1971 году самолеты были доработаны для подвески специальных «термостатических» фугасных авиабомб, которые можно было сбрасывать из стратосферы на сверхзвуковой скорости. Четыре МиГ-25РБ (т.е. «разведчика-бомбардировщика», или «Изделие 02Б») передали в 1971 году в Египет, чтобы тот мог использовать их для ударов по Израилю. Однако в ВВС арабских стран эти машины выполняли лишь разведывательные полеты.

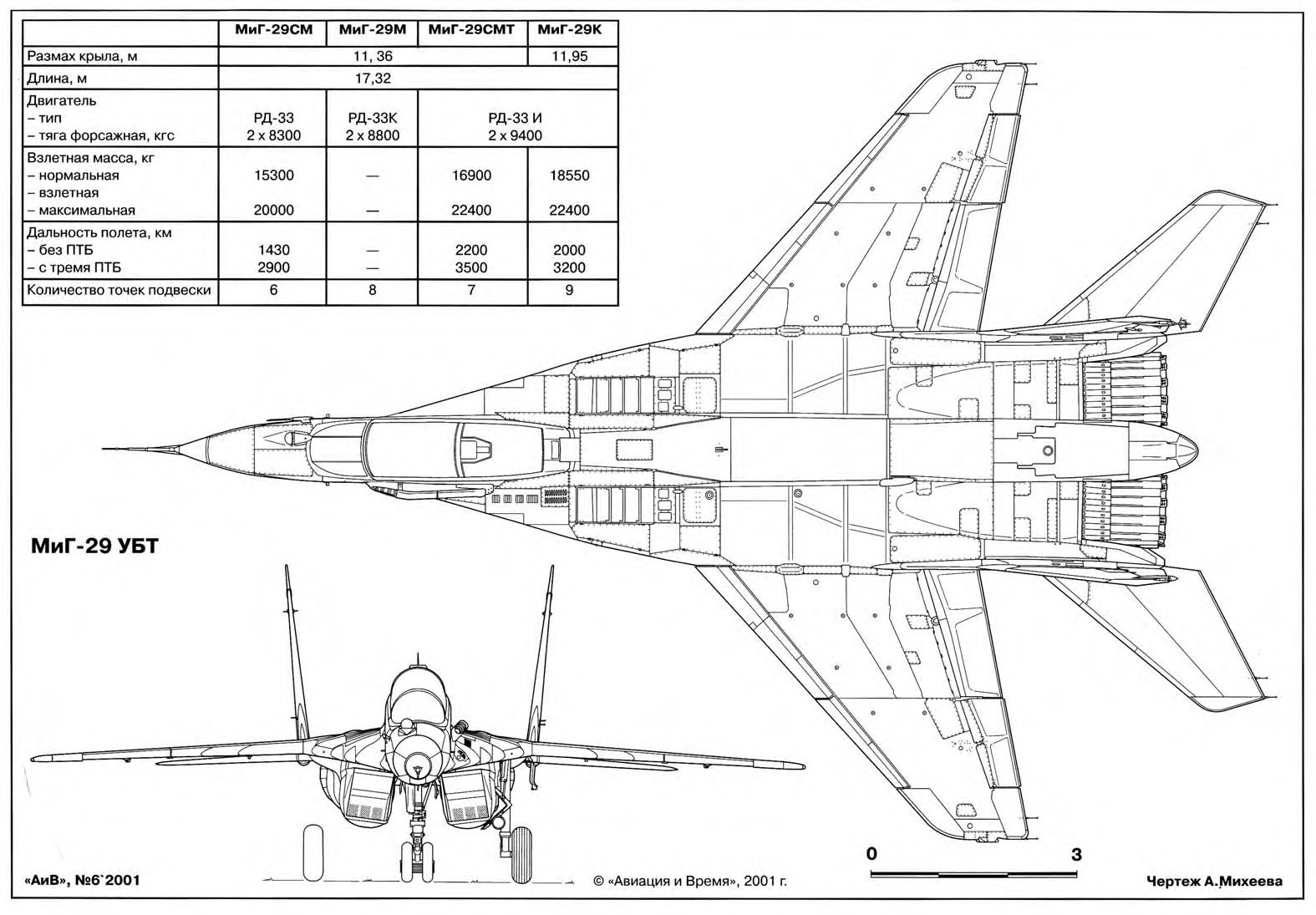
Все дальнейшие модели выпускались уже как разведчики-бомбардировщики, и отличались только составом радиотехнического разведывательного оборудования. Так, вариант с аппаратурой точной радиотехнической разведки «Куб-3» получил индекс МиГ-25РБК, с РЛС бокового обзора «Сабля Е» — МиГ-25РБС, со станцией общей радиотехнической разведки «Вираж-1» — МиГ-25РБВ, с РЛС бокового обзора «Шомпол» — МиГ-25РБШ. Для подготовки и тренировки пилотов был создан также двухместный «учебный» вариант МиГ-25РУ (выпускалась с 1972 года).

На специальных вариантах МиГ-25 было установлено 29 мировых рекордов, среди которых — абсолютный рекорд высоты полета — 37   650 метров.

На Горьковском авиазаводе в 1969-85 гг было выпущено 1 186 самолетов типа МиГ-25 (всех моделей), находившихся на вооружении ВВС 14 стран мира.

ВВС Украины в 1992 году имели около 100 самолетов типа МиГ-25 (из них 13 МиГ-25 РБ и 2 МиГ-25РУ). До середины 90-х годов они постепенно были сняты с вооружения. Однако на Запорожском АРЗ продолжают выполнять ремонт этих машин для ВВС Индии и арабских стран.

В дальнейшем в музее планируется создать отдельную коллекцию основных моделей самолета МиГ-25.

Первый полет: 06 марта 1964 г.
Экипаж: 1 чел.
Двигатели: Р-15Б-300, 2 х 11 200 кгс
Длина (с ППТ): 21.55 м
Размах крыла: 13.38 м
Площадь крыла: 58.9 м2
Взлетный вес: нормальный — 37 100 кг, максимальный — 41 200 кг
Максимальная скорость: 3000 км/ч (М=2.9)
Практический потолок: 23 000 м
Дальность полета: 1860 км (с ППБ — 2400 км)
Разбег/пробег: 1200/800 м
Вооружение: аэрофотоаппараты А-70М, АФА-72, НА-75, А/Е-10, станция радиотехнической разведки CРС-4А/Б, бомбы общим весом до 5000 кг
Серийное производство: 1969-85 гг. Всего выпущено 1186 самолетов типа МиГ-25 всех моделей, которые находились на вооружении ВВС 10 государств мира. ВВС Украины в 1992 г. имели свыше 100 самолетов типа МиГ-25

Самолет МиГ-25

› Пистолеты

› Автоматы

› Снайперские винтовки

› Пулеметы

› Пистолет-пулеметы

› Крупнокалиберные пулеметы и пушки

› Гранатометы

› Боеприпасы

› Обучение стрельбе

› Самоходные артиллерийские установки

› Гаубицы

› Минометы

› Зенитно-ракетные комплексы

› Бронетранспортеры

› Боевые машины пехоты

› Танки

› Системы залпового огня

› Управляемое вооружение

› Самолеты

› Вертолеты

› БПЛА

› Авиационные ракеты

› Авиация 1910-1917

› Дни Воинской Славы

› Исторические события

› Военные праздники

› Важные даты России

› Дни рождения

› Православные праздники

› Международные праздники

› Народные праздники

› Церковный календарь 2023

› Спецслужбы России

› Спецслужбы Мира

› Операции спецслужб

› История первой мировой войны

› Сражения Первой мировой

› Полководцы Первой мировой

› История второй мировой войны

› Сражения второй мировой

› Полководцы второй мировой

› История авиации

› Оружие Победы

› Великие сражения

› Биографии великих людей

› Памяти товарищей

› Великие разведчики

› Действия при ЧС

› Анатомия человека

› Доврачебная помощь

› Награды Российской Империи

› Ордена СССР

› Медали СССР

› Юбиленые медали СССР

› Ордена России

› Медали России

› Юбилейные медали России


МИГ-25—  советский сверхзвуковой высотный истребитель-перехватчик 3-го поколения.

Истребитель МИГ-25 предназначен:

► для ведения воздушной оптической, радиотехнической и радиолокационной разведки с больших высот

► для нанесения бомбовых ударов по стационарным и площадным наземным целям

Летно-технические характеристики МИГ-25:

Экипаж: 1 человек

Длина самолета: 19,75 м

Высота самолета: 5,14 м

Размах крыла: 14,02 м

Площадь крыла: 61,40 м2

Нормальная взлетная масса:

36 720 кг

Взлетная масса без внешних подвесок: 34 920 кг

Топлива во внутренних баках: 14 570 кг

Топлива во внутренних баках и ПТБ: 19 450 кг

Максимальная скорость: 3 000 км/ч

Максимальная скорость у земли: 1 200 км/ч

Практический потолок: 20 700 м

Практическая дальность на сверхзвуковой скорости: 1 250 км

Практическая дальность на дозвуковой скорости: 1 730 км

Продолжительность полета: 2 часа

Длина разбега: 1 250 м

Длина пробега с тормозным парашютом: 800 м

Максимальная эксплуатационная перегрузка: +3,8G

Самолет МИГ-25 выполнен по системе  монокока с верхним расположением крыла и двумя килями.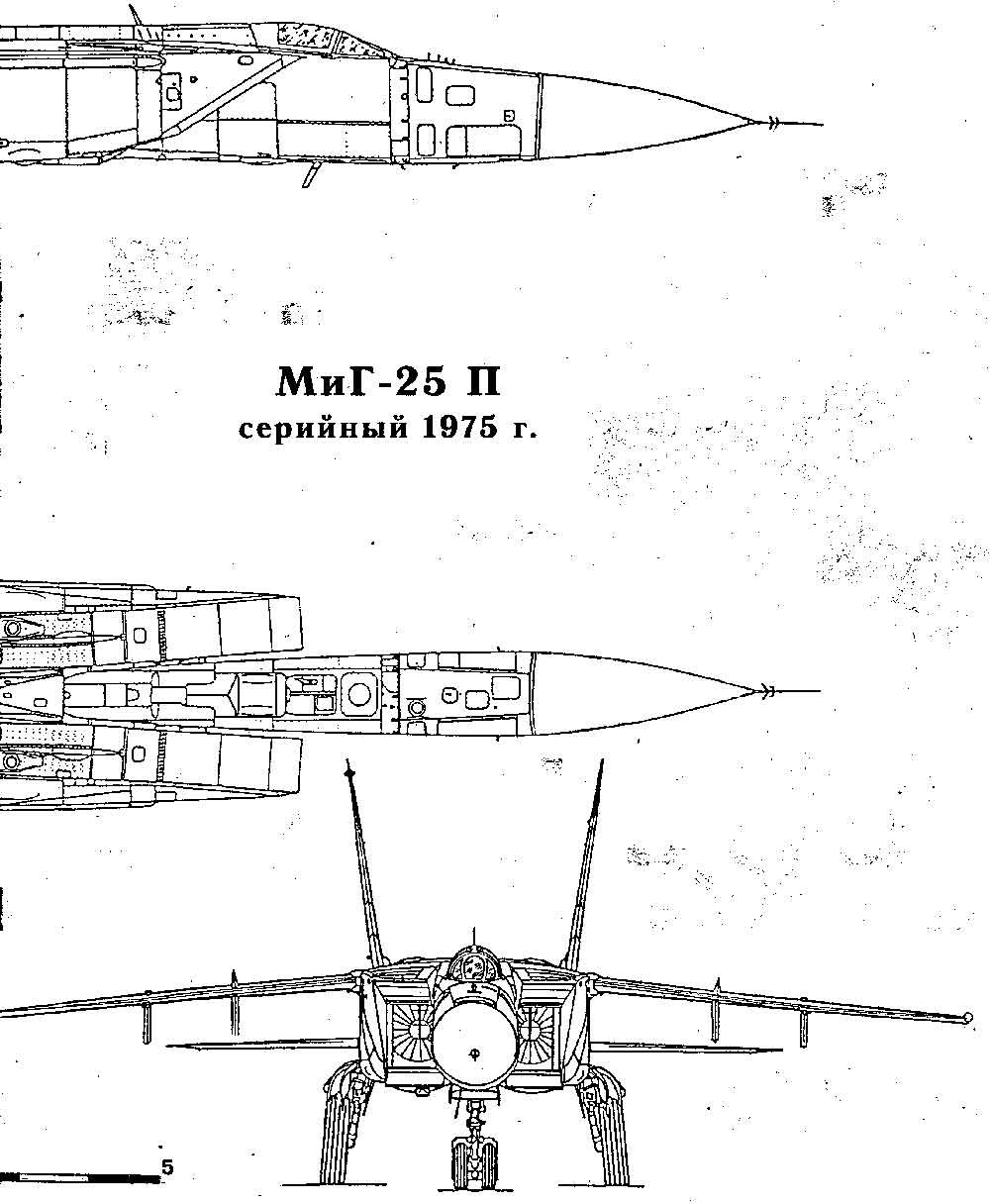  На МИГ-25 использован титан и нержавеющая сталь.

В 1976 году самолет МИГ-25П был угнан в Японию

лейтенантом В. Беленко, ставшим предателем СССР.

Вооружение МИГ-25:

► ракеты на 4-х уздах внешней подвески

Материал подготовлен на основе информации из открытых источников

МИГ Самолеты России истребитель истребитель-перехватчик Самолеты

Смотреть еще

Самолеты

e-mail: [email protected]

Материалы данного сайта размещаются только для ознакомления и не являются публичным призывом к выполнению каких-либо действий. Ресурс крайне осуждает любые формы экстремизма и терроризма.


Стальные C-образные каналы

по американскому стандарту.

Свойства С-образных профилей American Steel в британских единицах измерения указаны ниже.

Для полной таблицы со статическими параметрами Момент инерции и Модуль упругого сечения — поверните экран!

9 0027 I x
(в 4 ) 9001 2 9011 3 2,600 900 12 90 113 13,4 9011 3 5,51 9011 3 8,14 9011 3 6,08 9001 9 90 113 9 0113 0,184 90 113 9096 1
  • 1 см 4 = 10 -8 м = 10 4 мм
  • 1 дюйм 4 = 4,16×10 5 мм 4 9005 7 = 41,6 см 4
  • 1 см 3 = 10 -6 м = 10 3 мм

 луч глубина 5 дюймов , вес 9 фунтов/фут .

Балки двутаврового сечения:

  • Великобритания: универсальные балки (UB) и универсальные колонны (UC)
  • Европа: IPE. ОН. ХЛ. HD и другие профили
  • US: широкий фланец (WF) и профили H

Вставьте каналы в модель Sketchup с помощью расширения Sketchup Engineering ToolBox

Функция создания момента | Определение, свойства, примеры

Марко Табога, доктор философии

Функция создания момента (mgf) — это функция, часто используемая для характеристики распределение случайной величины.

Содержание

  1. Способ применения

  2. Определение

  3. Пример

  4. Получение моментов с помощью мгс

  5. Характеристика распределения с помощью функции генерации момента

  6. Подробнее

    1. Производящая функция момента линейного преобразования

    2. Производящая момент функция суммы взаимно независимых случайных величин

    3. Многомерное обобщение

  7. Решенные упражнения

    1. Упражнение 1

    2. Упражнение 2

    3. Упражнение 3

  8. 90 002 Каталожные номера

Как используется

Функция создания момента имеет большое практическое значение, поскольку:

  1. его можно использовать для легкого получения моментов; его производные в нуле равны моментам случайной величины;

  2. распределение вероятностей однозначно определяется его мгс.

Факт 2, в сочетании с аналитической податливостью MGFS, делает их удобными. инструмент для решения нескольких задач, таких как получение распределения суммы двух и более случайных величин.

Определение

Ниже приводится формальное определение.

Определение Позволять быть случайной величиной. Если ожидаемое значение существует и конечен для всех действительных чисел принадлежащий замкнутому интервалу , с , тогда мы говорим, что обладает производящей момент функцией и функция называется функцией генерации момента .

Не все случайные величины обладают производящей момент функцией. Однако все случайные величины обладают характеристикой функция, еще одно преобразование, обладающее свойствами, подобными тем, наслаждается мгф.

Пример

Следующий пример показывает, как мгс экспоненциального вычисляется случайная величина.

Пример Позволять быть непрерывной случайной величиной с поддержка и плотность вероятности функциягде является строго положительным числом. Ожидаемое значение можно вычислить как следует: Кроме того, указанное выше математическое ожидание существует и конечно для любого , предоставил . Как следствие, обладает мгф:

Получение моментов с помощью мгф

Функция генерации моментов получила свое название благодаря тому, что ее можно использовать для получения моментов , как указано в следующем предложении.

Предложение Если случайная величина обладает мгф , затем -й момент , обозначается , существует и конечен для любого . Кроме того, где это -й производная от в отношении , оценивается в точку .

Доказательство

Доказательство приведенного выше утверждения довольно сложно, потому что нужно позаботиться о многих аналитических деталях (см. например Пфайффер — 2012). Интуиция, однако, простой. Поскольку ожидаемое значение является линейным оператором и дифференцирование является линейной операцией, при соответствующих условиях мы можем дифференцировать через ожидаемое значение:Изготовление замена , мы получить

Следующий пример показывает, как можно применить это предложение.

Пример В предыдущем примере мы показали, что мгф экспоненциального случайная переменная это ожидаемая стоимость можно вычислить, взяв первую производную от мгф: и оценивая его в : второй момент можно вычислить, взяв вторую производную от мгф: и оценивая его в :И так далее для более высоких моментов.

Характеристика распределения через момент производящая функция

Важнейшим свойством MGF является следующее.

Предложение Позволять и быть двумя случайными величинами. Обозначим через и их распространение функции и и их мгфс. и имеют одинаковое распределение (т. для любого ) тогда и только тогда, когда они имеют одинаковые мгфс (т. е. для любого ).

Доказательство

Для полного общего доказательства этого предложение см., например, Feller (2008). Мы только дайте неформальное доказательство для частного случая, когда и дискретные случайные величины, принимающие только конечное число значений. «Только если» часть банальна. Если и имеют такое же распределение, затем Часть «если» доказывается следующим образом. Обозначим через и поддержка и и по и их вероятностная масса функции. Обозначим через союз двух поддерживает: и к элементы . мгф можно написать asBy тот же токен, мгф можно написать будто и иметь одинаковую мгс, то для любого принадлежащий к закрытому району г. ноль и перестановка условия, мы получить это может быть верным для любого принадлежащий только замкнутой окрестности нуля если для каждый . Отсюда следует, что функция массы вероятности и равны. Как следствие, равны и их функции распределения.

Это положение чрезвычайно важно и актуально с практической точки зрения: во многих случаях, когда нам нужно доказать, что два распределения равны, гораздо проще доказать равенство производящих функций моментов чем доказывать равенство функций распределения.

Также отметим, что равенство функций распределения можно заменить в предложение выше от:

Подробнее

Следующие разделы содержат более подробную информацию о файле mgf.

Функция создания момента линейное преобразование

Позволять быть случайной величиной, обладающей .

определитьгде две константы и .

Тогда случайная величина обладает мгф и

Доказательство

По самому определению мгф мы естьОчевидно, если определяется на замкнутом интервале , затем определяется на интервале .

Функция создания момента сумма взаимно независимых случайных величин

Позволять , …, быть взаимно независимые случайные величины.

Позволять быть их сумма:

Тогда мгф является произведением мгфс , …, :

Доказательство

Это легко доказать с помощью определение мгф и свойства взаимно независимых переменные:

Многомерное обобщение

Многомерное обобщение МГФ обсуждается в лекции о соединение производящая момент функция.

Решенные упражнения

Некоторые решенные упражнения на производящие функции моментов можно найти ниже.

Упражнение 1

Позволять быть дискретной случайной величиной, имеющей Распределение Бернулли.

Его поддержка остров его вероятностная масса функция это здесь является константой.

Выведите производящую функцию момента , если он существует.

Решение

По определению образующего момента функция, мы естьОчевидно, производящая функция момента существует, и она определена корректно, поскольку приведенное выше ожидаемое значение существует для любого .

Упражнение 2

Позволять быть случайной величиной с порождающим моментом функция

Получите дисперсию .

Решение

Мы можем использовать следующую формулу для вычисление дисперсия: ожидаемая стоимость вычисляется путем взятия первой производной момента, образующего функция: и оценивая его в : второй момент вычисляется путем взятия второй производной момента, порождающего функция: и оценивая его в : Следовательно,

Упражнение 3

Случайная величина говорят, что имеет распределение хи-квадрат с степеней свободы, если его производящая функция момента определена для любого и это равно до

Определять где и две независимые случайные величины, имеющие распределение хи-квадрат с и степеней свободы соответственно.

Докажи это имеет распределение хи-квадрат с степени свободы.

Решение

Момент производящие функции и являются производящая функция момента суммы независимых случайных величин есть просто произведение их моментов, порождающих функции: Следовательно, — производящая момент функция случайной величины хи-квадрат с степени свободы. Как следствие, имеет распределение хи-квадрат с степени свободы.

Ссылки

Феллер, В. (2008) Введение к теории вероятностей и ее приложениям, том 2, Wiley.

Пфайффер, ЧП (1978) Концепции теория вероятностей, Dover Publications.

Как цитировать

Пожалуйста, указывайте как:

Taboga, Marco (2021). «Производящая функция момента», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/fundamentals-of-probability/moment-generating-function.

Обозначение Размеры Статические параметры
Момент инерции Модуль упругого сечения
Имперский
(дюйм x фунт/фут) 		Глубина
— h —
(дюйм)
С
— w —
(дюйм) 90 028		 Толщина стенки
— s —
(в )
Площадь сечения
(в 2 ) 		Вес
(фунт f /фут) 		I г
(в 4 ) 		S x
(в 3 ) 		S y
900 64 (в 3 )
C 15 x 50 15 3,716 0,716 14,7 50 404 11,0 53,8 3,7 8
C 15 x 40 15 3,520 0,520 11,8 40 349 9,23 46,5 3,37
C 15 x 33,9 15 3,400 0,400 9,96 33,9 315 8,13 42,0 3,11
     
C 12 x 30 12 3,170 0,510 8,82 30 162 5,14 27,0 2,06
C 12 x 25 12 3,047 0,387 7. 35 25 144 4,47 24,1 1,88
C 12 x 20,7 12 2,942 0,282 6,09 20,7 129 3,88 21,5 1,73
      9 C 1 0 x 30 10 3,033 0,673 8,82 30 103 3,94 20,7 1,65
С 10 х 25 10 2,886 0,526 7,35 25 91,2 3,36 18,2 1,48
C 10 x 20 10 2,739 0,379 5,88 20 78,9 2,81 15,8 1,32
C 10 x 15,3 10 0,240 4,49 15,3 67,4 2,28 13,5 1,16
     С 9 x 20 9 2,648 0,448 5,88 20 60,9 2,42 13,5 1,17
С 9 х 15 9 2,485 0,285 4,41 15 51,0 1,93 11,3 90 114 1,01
C 9 x 13,4 9 2,433 0,233 3,94 47,9 1,76 10,6 0,96
        90 114            
C 8 x 18,75 8 2,527 0,487 18,75 44,0 1,98 11,0 1,01
C 8 x 13 . 75 8 2,343 0,303 4,04 13,75 36,1 1,53 9,03 0,85
С 8 x 11,5 8 2,260 0,220 3,38 11,5 32,6 1,32 0,78
901 14        
C 7 x 14,75 7 2,299 0,419 4,33 14,75 27 .2 1,38 7,78 0,78
C 7 x 12,25 7 2,194 0,314 9011 С 7 х 9,8 7 2,090 0,210 2,87 9,8 21,3 0,97 0,63
   
C 6 x 13 6 2,157 0,437 3,83 13 17,4 901 14 1,05 5,80 0,64
C 6 x 10,5 6 2,034 0,314 3,09 10,5 15,2 0,87 5,06 0,56
C 6 x 8,2 6 1,920 0,200 2,40 8,2 13,1 0,69 4,38 0,49
  90 114    
C 5 x 9 5 1,885 0,325 2,64 9 8,90 0,63 3,56 0,45
C 5 x 6,7 5 1,750 0,190 1,97 6,7 7,49 0. 48 3,00 0,38
C 4 x 7,25 4 1,721 0,321 2,13 7,25 4,59 0,43 2,29 0,34
C 4 x 5,4 4 1,584 1,59 5,4 3,85 0,32 1,93 0,28
C 3 x 6 3 1. 596 0,356 1,76 6 2,07 0,31 1,38 0,27 90 114
С 3 х 5 3 1,498 0,258 1,47 5 1,85 0,25 901 14 1,24 0,23
С 3 x 4,1 3 1,410 0,170 1,21 4,1 1,66 0,20 1,10 0,20